搜索
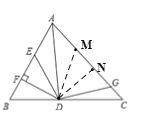
【题目】如图，AD是△ABC的角平分线，DF⊥AB，垂足为F，DE=DG，△ADG和△AED的面积分别为48和36，求△EDF的面积________.
参考答案：
【答案】6
【解析】
作DM=DE交AC于M，作DN⊥AC，利用角平分线的性质得到DN=DF，将三角形EDF的面积转化为三角形DNM的面积来求．
作DM=DE交AC于M，作DN⊥AC，
∵AD是△ABC的角平分线，DF⊥AB，
∴DF=DN，
∵DE=DG，
∴DG=DM，
∴Rt△DEF≌Rt△DMN（HL），
∵DG=DM， DN⊥AC，
∴MN=NG，
∴△DMN≌△DNG，
∵△ADG和△AED的面积分别为48和36，
∴S△MDG=S△ADG-S△ADM=48-36=12，
∴S△DEF=
S△MDG= 
12=6，
故答案为：6
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在平面直角坐标系中，抛物线经过坐标原点O，点A（6，﹣6
），且以y轴为对称轴．
（1）求抛物线的解析式；
（2）如图2，过点B（0，﹣ ）作x轴的平行线l，点C在直线l上，点D在y轴左侧的抛物线上，连接DB，以点D为圆心，以DB为半径画圆，⊙D与x轴相交于点M，N（点M在点N的左侧），连接CN，当MN=CN时，求锐角∠MNC的度数；
（3）如图3，在（2）的条件下，平移直线CN经过点A，与抛物线相交于另一点E，过点A作x轴的平行线m，过点（﹣3，0）作y轴的平行线n，直线m与直线n相交于点S，点R在直线n上，点P在EA的延长线上，连接SP，以SP为边向上作等边△SPQ，连接RQ，PR，若∠QRS=60°，线段PR的中点K恰好落在抛物线上，求Q点坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知△ABC的三个顶点的坐标分别为：A（﹣2，3）、B（﹣6，0）、C（﹣1，0）．
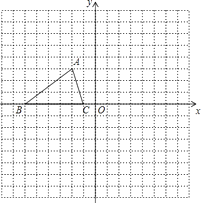
（1）将△ABC沿y轴翻折，画出翻折后的△A1B1C1 ， 点A的对应点A1的坐标是
（2）△ABC关于x轴对称的图形△A2B2C2 ， 直接写出点A2的坐标
（3）若△DBC与△ABC全等（点D与点A重合除外），请直接写出满足条件点D的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，AB=AC，AD⊥BC，CE⊥AB，AE=CE．求证：
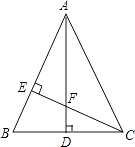
（1）△AEF≌△CEB；
（2）AF=2CD． -
科目： 来源： 题型：
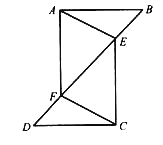
查看答案和解析>>【题目】如图，已知△ABF≌△CDE.
（1）若∠B＝30°，∠DCF＝40°，求∠EFC的度数；
（2）若BD=10，EF=2，求BF的长.
-
科目： 来源： 题型：
查看答案和解析>>【题目】有两块面积相同的试验田，分别收获蔬菜900kg和1500kg，已知第一块试验田每亩收获蔬菜比第二块少300kg，求第一块试验田每亩收获蔬菜多少千克？
-
科目： 来源： 题型：
查看答案和解析>>【题目】根据题意解答
（1）如图1，在四边形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°，E、F分别是BC、CD上的点，且∠EAF=60°，延长FD到点G，使DG=BE，连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得线段BE、EF、FD之间的数量关系为 ．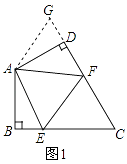
（2）如图2，在四边形ABCD中，AB=AD，∠B+∠D=180°，E、F分别是BC、CD上的点，且∠EAF=
∠BAD，线段BE、EF、FD之间存在什么数量关系，为什么？
（3）如图3，点A在点O的北偏西30°处，点B在点O的南偏东70°处，且AO=BO，点A沿正东方向移动249米到达E处，点B沿北偏东50°方向移动334米到达点F处，从点O观测到E、F之间的夹角为70°，根据（2）的结论求E、F之间的距离．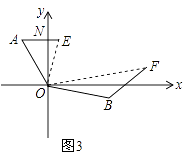
相关试题
