Question

【题目】已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论：①b＜0，c＞0；②a+b+c＜0；③方程的两根之和大于0；④a﹣b+c＜0，其中正确的个数是（ ）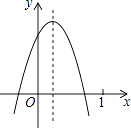

A.4个
B.3个
C.2个
D.1个

Answer 1

【答案】B
【解析】解：∵抛物线开口向下，
∴a＜0，
∵抛物线对称轴x＞0，且抛物线与y轴交于正半轴，
∴b＞0，c＞0，故①错误；
由图象知，当x=1时，y＜0，即a+b+c＜0，故②正确，
令方程ax2+bx+c=0的两根为x1、x2 ，
由对称轴x＞0，可知 ＞0，即x1+x2＞0，故③正确；
由可知抛物线与x轴的左侧交点的横坐标的取值范围为：﹣1＜x＜0，
∴当x=﹣1时，y=a﹣b+c＜0，故④正确．
故选：B．
【考点精析】本题主要考查了二次函数图象以及系数a、b、c的关系的相关知识点，需要掌握二次函数y=ax2+bx+c中，a、b、c的含义：a表示开口方向：a>0时，抛物线开口向上; a<0时，抛物线开口向下b与对称轴有关：对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标：（0，c）才能正确解答此题．