【题目】如图,在△ABC中,BO、CO分别平分∠ABC和∠ACB.计算:
(1)若∠A=60°,求∠BOC的度数;
(2)若∠A=100°,则∠BOC的度数是多少?
(3)若∠A=120°,则∠BOC的度数又是多少?
(4)由(1)、(2)、(3),你发现了什么规律?请用一个等式将这个规律表示出来.

参考答案:
【答案】(1)120°;(2)140°;(3)150°;(4)90°+![]() ∠A.
∠A.
【解析】
1)根据角平分线的定义和三角形的内角和定理求出∠OBC+∠OCB的值,再利用三角形的内角和定理求出∠BOC的值;
(2)先根据角平分线的定义得到∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,再根据三角形内角和定理得到∠BOC=180°-(∠OBC+∠OCB),∠ABC+∠ACB=180°-∠A,则∠BOC=180°-
∠ACB,再根据三角形内角和定理得到∠BOC=180°-(∠OBC+∠OCB),∠ABC+∠ACB=180°-∠A,则∠BOC=180°-![]() (180°-∠A)=90°+
(180°-∠A)=90°+![]() ∠A,然后把∠A的度数代入计算即可;(3)同(2)的计算方法;(4)根据(1)(2)(3)的结论即可得到结果.
∠A,然后把∠A的度数代入计算即可;(3)同(2)的计算方法;(4)根据(1)(2)(3)的结论即可得到结果.
(1)∵BO、CO分别平分∠ABC和∠ACB,∠A=60°,
∴∠CBO+∠BCO=![]() (180°﹣∠A)=
(180°﹣∠A)=![]() (180°﹣60°)=60°,
(180°﹣60°)=60°,
∴∠BOC=180°﹣(∠CBO+∠BCO)=180°﹣60°=120°;
(2)同理,若∠A=100°,则∠BOC=180°﹣![]() (180°﹣∠A)=90°+
(180°﹣∠A)=90°+![]() ∠A=140°;
∠A=140°;
(3)同理,若∠A=120°,则∠BOC=180°﹣![]() (180°﹣∠A)=90°+
(180°﹣∠A)=90°+![]() ∠A=150°;
∠A=150°;
(4)由(1)、(2)、(3),发现:∠BOC=180°﹣![]() (180°﹣∠A)=90°+
(180°﹣∠A)=90°+![]() ∠A.
∠A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明家门前有一条小河,村里准备在河面上架上一座桥,但河宽AB无法直接测量,爱动脑的小明想到了如下方法:在与AB垂直的岸边BF上取两点C、D使CD= ,再引出BF的垂线DG,在DG上取一点E,并使A、C、E在一条直线上,这时测出线段 的长度就是AB的长.
(1)按小明的想法填写题目中的空格;
(2)请完成推理过程.

-
科目: 来源: 题型:
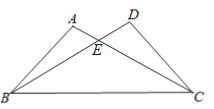
查看答案和解析>>【题目】如图,已知∠A=∠D有下列五个条件①AE=DE ②BE=CE ③AB=DC ④∠ABC=∠DCB⑤AC=BD能证明△ABC与△DCB全等的条件有几个?并选择其中一个进行证明。
-
科目: 来源: 题型:
查看答案和解析>>【题目】y=
 x+1是关于x的一次函数,则一元二次方程kx2+2x+1=0的根的情况为( )
x+1是关于x的一次函数,则一元二次方程kx2+2x+1=0的根的情况为( )
A.没有实数根
B.有一个实数根
C.有两个不相等的实数根
D.有两个相等的实数根 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为x,两个三角形重叠面积为y,则y关于x的函数图象是( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①b<0,c>0;②a+b+c<0;③方程的两根之和大于0;④a﹣b+c<0,其中正确的个数是( )
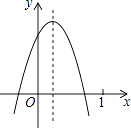
A.4个
B.3个
C.2个
D.1个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠B=30°,AB的垂直平分线ED交AB于点E,交BC于点D,若CD=3,则BD的长为 .

相关试题

