【题目】为解决都匀市停车难的问题,计划在一段长为56米的路段规划处如图所示的停车位,已知每个车位是长为5米,宽为2米的矩形,且矩形的宽与路的边缘成45°角,则该路段最多可以划出个这样的停车位.(取 ![]() =1.4,结果保留整数)
=1.4,结果保留整数) 
参考答案:
【答案】19
【解析】解:如图, 
∵CE=2,DE=5,且∠BCE=∠CBE=∠ABD=∠ADB=45°,
∴BE=CE=2,BD=DE﹣BE=3,
∴BC=2÷sin45°=2 ![]() ,AB=(5﹣2)×sin45°=(5﹣2)×
,AB=(5﹣2)×sin45°=(5﹣2)× ![]() =
= ![]() ,
,
设至多可划x个车位,依题意可列不等式
2 ![]() x+
x+ ![]() ≤56,
≤56,
将 ![]() =1.4代入不等式,化简整理得,28x≤539,
=1.4代入不等式,化简整理得,28x≤539,
解得x≤19 ![]() ,因为是正整数,所以x=19,
,因为是正整数,所以x=19,
所以这个路段最多可以划出19个这样的停车位.
故答案为:19.
如图,根据三角函数可求BC,AB,设至多可划x个车位,依题意可列不等式2 ![]() x+(5﹣2)×
x+(5﹣2)× ![]() ≤56,解不等式即可求解.考查了解直角三角形的应用,主要是三角函数及运算,关键把实际问题转化为数学问题加以计算.
≤56,解不等式即可求解.考查了解直角三角形的应用,主要是三角函数及运算,关键把实际问题转化为数学问题加以计算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①b<0,c>0;②a+b+c<0;③方程的两根之和大于0;④a﹣b+c<0,其中正确的个数是( )
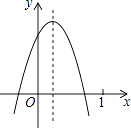
A.4个
B.3个
C.2个
D.1个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠B=30°,AB的垂直平分线ED交AB于点E,交BC于点D,若CD=3,则BD的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的对角线AC的中点为O,过点O作OE⊥BC于点E,连接OD,已知AB=6,BC=8,则四边形OECD的周长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上):
①把△ABC沿BA方向平移,请在网格中画出当点A移动到点A1时的△A1B1C1;
②把△A1B1C1绕点A1按逆时针方向旋转90°后得到△A2B2C2 , 如果网格中小正方形的边长为1,求点B1旋转到B2的路径长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图四边形ABCD中,AD∥BC,∠BCD=90°,∠BAD的平分线AG交BC于点G.
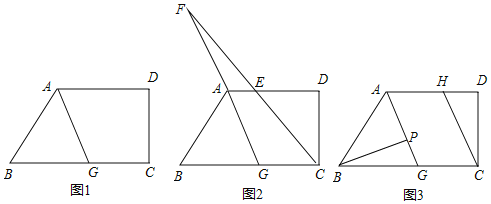
(1)求证:∠BAG=∠BGA;
(2)如图2,∠BCD的平分线CE交AD于点E,与射线GA相交于点F,∠B=50°.
①若点E在线段AD上,求∠AFC的度数;
②若点E在DA的延长线上,直接写出∠AFC的度数;
(3)如图3,点P在线段AG上,∠ABP=2∠PBG,CH∥AG,在直线AG上取一点M,使∠PBM=∠DCH,请直接写出∠ABM:∠PBM的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
 .
.
相关试题

