【题目】已知有理数a、b在数轴上的对应点如图所示.
(1)已知a=–2.3,b=0.4,计算|a+b|–|a|–|1–b|的值;
(2)已知有理数a、b,计算|a+b|–|a|–|1–b|的值.
![]()
参考答案:
【答案】(1)-1;(2)-1.
【解析】
(1)根据a、b的值可以求出所求式子的值;
(2)根据数轴可以判断a、b的正负,从而可以求得所求式子的值.
(1)当a=﹣2.3,b=0.4时,
|a+b|﹣|a|﹣|1﹣b|
=|﹣2.3+0.4|﹣|﹣2.3|﹣|1﹣0.4|
=1.9﹣2.3﹣0.6
=﹣1;
(2)由数轴可得:a<﹣1<0<b<1,∴a+b<0,a<0,1﹣b>0,∴|a+b|﹣|a|﹣|1﹣b|
=﹣(a+b)﹣(﹣a)﹣(1﹣b)
=﹣a﹣b+a﹣1+b
=﹣1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)操作发现:
如图,在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G.猜想线段GF与GC有何数量关系?并证明你的结论.

(2)类比探究:
如图,将(1)中的矩形ABCD改为平行四边形,其它条件不变,(1)中的结论是否仍然成立?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】用适当的方法解一元二次方程
(1)x2+3x+1=0
(2)(x﹣1)(x+2)=2(x+2) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,直线EF与AB、CD分别相交于点E、F.
(1)如图1,若∠1=120°,∠2=60°,求证AB∥CD;
(2)在(1)的情况下,若点P是平面内的一个动点,连结PE、PF,探索∠EPF、∠PEB、∠PFD三个角之间的关系;
①当点P在图2的位置时,可得∠EPF=∠PEB+∠PFD;
请阅读下面的解答过程,并填空(理由或数学式)
解:如图2,过点P作MN∥AB,
则∠EPM=∠PEB_____.
∵AB∥CD(已知),MN∥AB(作图)
∴MN∥CD_____.
∴∠MPF=∠PFD
∴∠_____+∠_____=∠PEB+∠PFD(等式的性质)
即∠EPF=∠PEB+∠PFD
②当点P在图3的位置时,∠EPF、∠PEB、∠PFD三个角之间有何关系并证明.
③当点P在图4的位置时,请直接写出∠EPF、∠PEB、∠PFD三个角之间的关系:_____.




-
科目: 来源: 题型:
查看答案和解析>>【题目】己知一元二次方程x2﹣3x+m﹣1=0.
(1)若方程有两个不相等的实数根,求实数m的取值范围;
(2)若方程有两个相等的实数根,求此时方程的根. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(﹣8,0),直线BC经过点B(﹣8,6),C(0,6),将四边形OABC绕点O按顺时针方向旋转角度α得到四边形OA′B′C′,此时边OA′与边BC交于点P,边B′C′与BC的延长线交于点Q,连接AP.
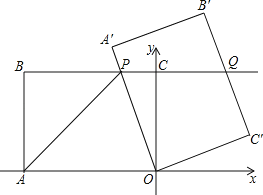
(1)四边形OABC的形状是 .
(2)在旋转过程中,当∠PAO=∠POA,求P点坐标.
(3)在旋转过程中,当P为线段BQ中点时,连接OQ,求△OPQ的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的口袋里装有仅颜色不同的黑、白两种颜色的球20只,某学习小组做摸球实验.将球搅匀后从中随机摸出一个球,记下颜色,再把它放回袋中,不断重复,下表是活动进行中记下的一组数据
摸球的次数

100
150
200
500
800
1000
摸到白球的次数

58
96
116
295
484
601
摸到白球的频率

0.58
0.64
0.58
0.59
0.605
0.601
(1)请你估计,当n很大时,摸到白球的频率将会接近 (精确到0.1).
(2)假如你去摸一次,你摸到白球的概率是 ,摸到黑球的概率是 .
(3)试估算口袋中黑、白两种颜色的球有多少只.
相关试题

