【题目】已知,如图,∠BAE+∠AED=180°,∠1=∠2,那么∠M=∠N(下面是推理过程,请你填空).
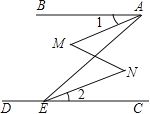
解:∵∠BAE+∠AED=180°(已知)
∴ ∥ (同旁内角互补,两直线平行)
∴∠BAE= (两直线平行,内错角相等)
又∵∠1=∠2
∴∠BAE﹣∠1= ﹣
即∠MAE=
∴ ∥ (内错角相等,两直线平行)
∴∠M=∠N(两直线平行,内错角相等)
参考答案:
【答案】AB,CD,∠AEC,∠AEC,∠2,∠AEN,AE,EN
【解析】
试题分析:由于∠BAE+∠AED=180°,根据平行线的判定定理可知AB∥CD,则∠BAE=∠AEC,因为∠1=∠2,可推出∠MAE=∠AEN,AM∥EN,∠M=∠N.
解:∵∠BAE+∠AED=180°(已知)
∴AB∥CD(同旁内角互补,两直线平行)
∴∠BAE=∠AEC(两直线平行,内错角相等)
又∵∠1=∠2
∴∠BAE﹣∠1=∠AEC﹣∠2
即∠MAE=∠AEN
∴AM∥EN(内错角相等,两直线平行)
∴∠M=∠N(两直线平行,内错角相等).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在多项式
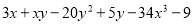 中,
中, 表示这个多项式的项数,
表示这个多项式的项数, 表示这个多项式中三次项的系数.在数轴上点
表示这个多项式中三次项的系数.在数轴上点 与点
与点 所表示的数恰好可以用
所表示的数恰好可以用 与
与 分别表示.有一个动点
分别表示.有一个动点 从点
从点 出发,以每秒2个单位长度的速度沿数轴向左匀速运动,设运动时间为
出发,以每秒2个单位长度的速度沿数轴向左匀速运动,设运动时间为 秒.
秒.(1)
 ________,
________, ___________,线段
___________,线段 _________个单位长度;
_________个单位长度;(2)点
 所表示数是________(用含
所表示数是________(用含 的多项式表示);
的多项式表示);(3)求当
 为多少时,线段
为多少时,线段 的长度恰好是线段
的长度恰好是线段 长度的三倍?
长度的三倍? -
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD、正方形BEFG和正方形DMNK的位置如图所示,点A在线段NF上,AE=8,则△NFP的面积为( ).
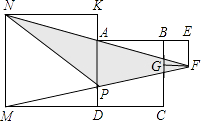
A.30
B.32
C.34
D.36 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6
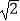 ,那么AC= .
,那么AC= . 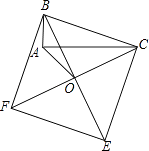
-
科目: 来源: 题型:
查看答案和解析>>【题目】解决问题:
一辆货车从超市出发,向东走了3千米到达小彬家,继续走2.5千米到达小颖家,然后向西走了10千米到达小明家,最后回到超市.
(1)以超市为原点,以向东的方向为正方向,用1个单位长度表示1千米,在数轴上表示出小明家,小彬家,小颖家的位置.
(2)小明家距小彬家多远?
(3)货车一共行驶了多少千米?
(4)货车每千米耗油0.2升,这次共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠A=36°,DE是AC的垂直平分线.

(1)求证:△BCD是等腰三角形;
(2)△BCD的周长是a,BC=b,求△ACD的周长(用含a,b的代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角坐标系中,
 的顶点坐标都在网格点上,其中点C的坐标为
的顶点坐标都在网格点上,其中点C的坐标为 ,
,
(1)写出点A,B的坐标

(2)将
 先向左平移2个单位长度,再向上平移1个单位长度,得到
先向左平移2个单位长度,再向上平移1个单位长度,得到 ,则
,则 的三个顶点坐标分别是
的三个顶点坐标分别是
(3)计算
 的面积.
的面积.
相关试题

