【题目】正方形ABCD、正方形BEFG和正方形DMNK的位置如图所示,点A在线段NF上,AE=8,则△NFP的面积为( ).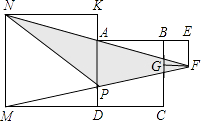
A.30
B.32
C.34
D.36
参考答案:
【答案】B
【解析】四边形BEFG、DMNK、ABCD是正方形,
∴∠E=∠F=90,AE∥MC,MC∥NK,
∴AE∥NK,
∴∠KNA=∠EAF,
∴△KNA∽△EAF,
∴NK:EA=KA:EF,
设BE=x,则AB=8x,NK=y,KA=y(8x)=x+y8,
∴![]() =
=![]()
∴![]() =
=![]() +1,
+1,
观察可知:当y=8时,等式成立,
∴y=8,
∴NK=AE,
∴△KNA≌△EAF,
∴NA=AF
∴FP=PM,
∴S△MNP=S△NPF,
∴S正方形DMNK=2S△MNP=64,
∴S△MNP=32,
∴S△NPF=32.
所以答案是:B.
【考点精析】本题主要考查了平行线的判定与性质和正方形的性质的相关知识点,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OM平分∠AOB,MC∥OB,MD⊥OB于D,若∠OMD=75°,OC=8,则MD的长为( )

A.2 B.3 C.4 D.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两辆公共汽车分别自A、B两地同时出发,相向而行。甲车行驶85千米后与乙车相遇,然后继续前进。两车到达对方的出发点等候30分钟立即依原路返回。当甲车行驶65千米后又与乙车相遇,求A、B两地的距离。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在多项式
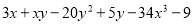 中,
中, 表示这个多项式的项数,
表示这个多项式的项数, 表示这个多项式中三次项的系数.在数轴上点
表示这个多项式中三次项的系数.在数轴上点 与点
与点 所表示的数恰好可以用
所表示的数恰好可以用 与
与 分别表示.有一个动点
分别表示.有一个动点 从点
从点 出发,以每秒2个单位长度的速度沿数轴向左匀速运动,设运动时间为
出发,以每秒2个单位长度的速度沿数轴向左匀速运动,设运动时间为 秒.
秒.(1)
 ________,
________, ___________,线段
___________,线段 _________个单位长度;
_________个单位长度;(2)点
 所表示数是________(用含
所表示数是________(用含 的多项式表示);
的多项式表示);(3)求当
 为多少时,线段
为多少时,线段 的长度恰好是线段
的长度恰好是线段 长度的三倍?
长度的三倍? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6
 ,那么AC= .
,那么AC= . 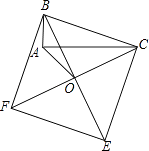
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,∠BAE+∠AED=180°,∠1=∠2,那么∠M=∠N(下面是推理过程,请你填空).
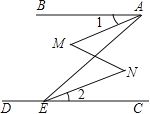
解:∵∠BAE+∠AED=180°(已知)
∴ ∥ (同旁内角互补,两直线平行)
∴∠BAE= (两直线平行,内错角相等)
又∵∠1=∠2
∴∠BAE﹣∠1= ﹣
即∠MAE=
∴ ∥ (内错角相等,两直线平行)
∴∠M=∠N(两直线平行,内错角相等)
-
科目: 来源: 题型:
查看答案和解析>>【题目】解决问题:
一辆货车从超市出发,向东走了3千米到达小彬家,继续走2.5千米到达小颖家,然后向西走了10千米到达小明家,最后回到超市.
(1)以超市为原点,以向东的方向为正方向,用1个单位长度表示1千米,在数轴上表示出小明家,小彬家,小颖家的位置.
(2)小明家距小彬家多远?
(3)货车一共行驶了多少千米?
(4)货车每千米耗油0.2升,这次共耗油多少升?
相关试题

