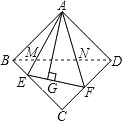
【题目】(1)如图①,在正方形ABCD中,△AEF的顶点E,F分别在BC,CD边上,高AG与正方形的边长相等,求∠EAF的度数.
(2)如图②,在Rt△ABD中,∠BAD=90°,AB=AD,点M,N是BD边上的任意两点,且∠MAN=45°,将△ABM绕点A逆时针旋转90°至△ADH位置,连接NH,试判断MN,ND,DH之间的数量关系,并说明理由.
(3)在图①中,连接BD分别交AE,AF于点M,N,若EG=4,GF=6,BM=3![]() ,求AG,MN的长.
,求AG,MN的长.

参考答案:
【答案】(1)45°(2)MN2=ND2+DH2(3)![]()
【解析】
试题分析:(1)根据高AG与正方形的边长相等,证明三角形全等,进而证明角相等,从而求出解.
(2)用三角形全等和正方形的对角线平分每一组对角的知识可证明结论.
(3)设出线段的长,结合方程思想,用数形结合得到结果.
试题解析:(1)在Rt△ABE和Rt△AGE中,AB=AG,AE=AE,
∴Rt△ABE≌Rt△AGE(HL).
∴∠BAE=∠GAE.
同理,∠GAF=∠DAF.
∴![]() .
.
(2)MN2=ND2+DH2.
∵∠BAM=∠DAH,∠BAM+∠DAN=45°,
∴∠HAN=∠DAH+∠DAN=45°.
∴∠HAN=∠MAN.
又∵AM=AH,AN=AN,
∴△AMN≌△AHN.
∴MN=HN.
∵∠BAD=90°,AB=AD,
∴∠ABD=∠ADB=45°.
∴∠HDN=∠HDA+∠ADB=90°.
∴NH2=ND2+DH2.
∴MN2=ND2+DH2.
(3)由(1)知,BE=EG,DF=FG.
设AG=x,则CE=x﹣4,CF=x﹣6.
在Rt△CEF中,
∵CE2+CF2=EF2,
∴(x﹣4)2+(x﹣6)2=102.
解这个方程,得x1=12,x2=﹣2(舍去负根).
即AG=12.
在Rt△ABD中,
∴![]() .
.
在(2)中,MN2=ND2+DH2,BM=DH,
∴MN2=ND2+BM2.
设MN=a,则![]() .
.
即a 2=(9![]() ﹣a) 2+(3
﹣a) 2+(3![]() ) 2,
) 2,
∴![]() .即MN=5
.即MN=5![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB⊥BD,CD⊥MN,垂足分别是B、D点,∠FDC=∠EBA.
(1)判断CD与AB的位置关系;
(2)BE与DF平行吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】当x=1时,代数式ax3+bx的值为﹣1,则当x=﹣1时,代数式ax3+bx﹣2的值为( )
A. ﹣4 B. ﹣3 C. ﹣2 D. ﹣1
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:a3﹣ab2= .
-
科目: 来源: 题型:
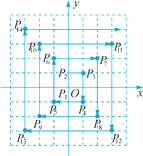
查看答案和解析>>【题目】如图,在平面直角坐标系中,每个最小方格的边长均为1个单位,P1,P2,P3,…均在格点上,其顺序按图中“→”方向排列,如:点P1(0,0),P2(0,1),P3(1,1),P4(1,-1),P5(-1,-1),P6(-1,2),….根据这个规律,求点P2018的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数据-3,-2,0,6,6,13,20,35则它的中位数和众数各是( )
A. 6和6 B. 3和6 C. 6和3 D. 9.5和6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线a∥b,∠3=131°,求∠1、∠2的度数(填理由或数学式)
解:∵∠3=131° ( )
又∵∠3=∠1 ()
∴∠1= ( )
∵a∥b ( )
∴∠1+∠2=180° ( )
∴∠2= ( ).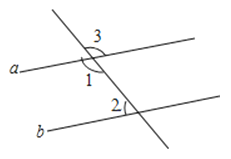
相关试题

