【题目】如图,已知矩形ABCD,点E为BC的中点,将△ABE沿直线AE折叠,点B落在B′点处,连接B′C

(1)求证:AE∥B′C;
(2)若AB=4,BC=6,求线段B′C的长。
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题(1)过E作EH⊥CF于H,由折叠的性质和点E是BC的中点以及矩形的性质可得△ABE∽△EHC,进而求得∠AEB=∠ECH,最后可得AE∥B′C;
(2)由(1)中的△ABE∽△EHC,即可求得线段B′C的长.
试题解析:

(1)证明:解:过E作EH⊥CF于H,
由折叠的性质得:BE=EF,∠BEA=∠FEA,
∵点E是BC的中点,
∴CE=BE,
∴EB′=CE,
∴∠B′EH=∠CEH,
∴∠AEB+∠CEH=90°,
在矩形ABCD中,
∵∠B=90°,
∴∠BAE+∠BEA=90°,
∴∠BAE=∠CEH,∠B=∠EHC,
∴△ABE∽△EHC,
∴∠AEB=∠ECH,
∴AE∥B′C;
(2)解:∵△ABE∽△EHC,
∴![]() ,
,
∴HC=![]() =
=![]() .
.
-
科目: 来源: 题型:
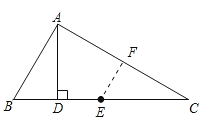
查看答案和解析>>【题目】如图,在△ABC中,若∠B=2∠C , AD⊥BC , E为BC边中点,求证:AB=2DE .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90,D是BC延长线上一点,E是BD的垂直平分线与AB的交点,DE交AC于点F,求证:EA=EF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】请回答下列问题:
(1)叙述三角形中位线定理,并运用平行四边形的知识证明;
(2)运用三角形中位线的知识解决如下问题:如图,在四边形ABCD中,AD∥BC , E、F分别是AB , CD的中点,求证:EF= (AD+BC)
(AD+BC)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=Rt∠,AC=8cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2cm,设运动的时间为t秒。

(1)当t为何值时,CP把△ABC的周长分成相等的两部分。
(2)当t为何值时,CP把△ABC的面积分成相等的两部分,并求出此时CP的长;
(3)当t为何值时,△BCP为等腰三角形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在梯形ABCD中,AD∥BC , AB=CD , ∠AOD=60°,E为OA的中点,F为OB的中点,G为CD的中点,试判断△EFG的形状并说明理由 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标中,已知点O(0,0),A(0,2),B(1,0),点P是反比例函数y=-

图象上的一个动点,过点P作PQ⊥x轴,垂足为Q . 若以点O、P、Q为顶点的三角形与△OAB相似,则相应的点P共有( ).
A.1个
B.2个
C.3个
D.4个
相关试题

