【题目】如图,在△ABC中,若∠B=2∠C , AD⊥BC , E为BC边中点,求证:AB=2DE . 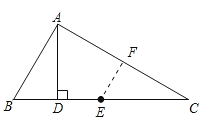
参考答案:
【答案】证明:取AC中点F , 连接EF , DF ,
则EF为中位线,且EF‖AB、∠FEC=∠B=2∠C ,
在直角三角形ACD中,F是斜边AC的中点,
∴DF=CF ,
∴∠DEF=∠C ,
即有2∠FDC=∠FEC ,
∴∠EFC=∠FDC+∠DFE ,
∴2∠DFE=∠FEC=2∠FDC ,
∴DE=EF ,
∴AB=2DE .
【解析】取AC中点F , 连接EF、DF , 则EF为△ABC的中位线,结合条件可得到∠FEC=2∠C , 结合直角三角形的性质可得到∠EDF=∠EFD , 得到DE=EF , 可得出结论 .
【考点精析】掌握三角形中位线定理是解答本题的根本,需要知道连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等边△ABC和等边△BPE,点P在BC的延长线上,EC的延长线交AP于M,连BM.
(1)求证:AP=CE;
(2)求∠PME的度数;
(3)求证:BM平分∠AME;
(4)AM,BM,MC之间有怎样的数量关系,直接写出,不需证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】梯形ABCD中AD∥BC , E是AB的中点,过E作两底的平行线交DC于F , 则下面结论错误的是( )
A.EF平分线段AC
B.梯形上下底间任意两点的连线段被EF平分
C.梯形EBCF与梯形AEFD周长之差的绝对值等于梯形两底之差的绝对值
D.梯形EBCF的面积比梯形AEFD的面积大 -
科目: 来源: 题型:
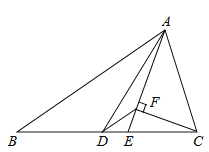
查看答案和解析>>【题目】如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F , AB=5,AC=2,则DF的长为.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90,D是BC延长线上一点,E是BD的垂直平分线与AB的交点,DE交AC于点F,求证:EA=EF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】请回答下列问题:
(1)叙述三角形中位线定理,并运用平行四边形的知识证明;
(2)运用三角形中位线的知识解决如下问题:如图,在四边形ABCD中,AD∥BC , E、F分别是AB , CD的中点,求证:EF= (AD+BC)
(AD+BC)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD,点E为BC的中点,将△ABE沿直线AE折叠,点B落在B′点处,连接B′C

(1)求证:AE∥B′C;
(2)若AB=4,BC=6,求线段B′C的长。
相关试题

