【题目】如图,在△ABC中,∠ACB=90,D是BC延长线上一点,E是BD的垂直平分线与AB的交点,DE交AC于点F,求证:EA=EF.

参考答案:
【答案】详见解析.
【解析】
过E作EG垂直于AC,交AC于G,可得出EG∥BD故∠AEG=∠B, ∠D=∠DEG.再根据E是BD的垂直平分线与AB的交点可得出∠B=∠D,根据ASA定理得出△AEG≌△FEG,进而可得出结论.
证明:过E作EG垂直于AC,交AC于G,
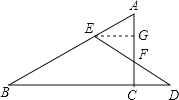
∵∠ACB=90°,
∴EG//BD,
∴∠AEG=∠B,∠D=∠DEG.
∵E是BD的垂直平分线与AB的交点,
∴BE=DE,
∴∠B=∠D,
∴∠AEG=∠DEG.
在△AEG与△FEG中,
∵∠AEG=∠FEG
EG=EG
∠AGE=∠FGE,
∴△AEG与△FEG (ASA),
∴EA=EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】梯形ABCD中AD∥BC , E是AB的中点,过E作两底的平行线交DC于F , 则下面结论错误的是( )
A.EF平分线段AC
B.梯形上下底间任意两点的连线段被EF平分
C.梯形EBCF与梯形AEFD周长之差的绝对值等于梯形两底之差的绝对值
D.梯形EBCF的面积比梯形AEFD的面积大 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F , AB=5,AC=2,则DF的长为.
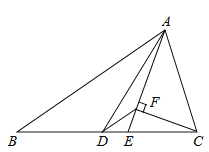
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,若∠B=2∠C , AD⊥BC , E为BC边中点,求证:AB=2DE .
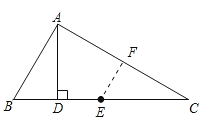
-
科目: 来源: 题型:
查看答案和解析>>【题目】请回答下列问题:
(1)叙述三角形中位线定理,并运用平行四边形的知识证明;
(2)运用三角形中位线的知识解决如下问题:如图,在四边形ABCD中,AD∥BC , E、F分别是AB , CD的中点,求证:EF= (AD+BC)
(AD+BC)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD,点E为BC的中点,将△ABE沿直线AE折叠,点B落在B′点处,连接B′C

(1)求证:AE∥B′C;
(2)若AB=4,BC=6,求线段B′C的长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=Rt∠,AC=8cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2cm,设运动的时间为t秒。

(1)当t为何值时,CP把△ABC的周长分成相等的两部分。
(2)当t为何值时,CP把△ABC的面积分成相等的两部分,并求出此时CP的长;
(3)当t为何值时,△BCP为等腰三角形?
相关试题

