【题目】已知二次函数![]() 经过点
经过点![]() 和点
和点![]() ,交
,交![]() 轴于
轴于![]() ,
,![]() 两点,交
两点,交![]() 轴于
轴于![]() ,则:①
,则:①![]() ;②无论
;②无论![]() 取何值,此二次函数图象与
取何值,此二次函数图象与![]() 轴必有两个交点,函数图象截
轴必有两个交点,函数图象截![]() 轴所得的线段长度必大于
轴所得的线段长度必大于![]() ;③当函数在
;③当函数在![]() 时,
时,![]() 随
随![]() 的增大而减小;④当
的增大而减小;④当![]() 时,
时,![]() ;⑤若
;⑤若![]() ,则
,则![]() .以上说法正确的有( )
.以上说法正确的有( )
A. ①②③④⑤ B. ①②④⑤ C. ②③④ D. ①②③⑤
参考答案:
【答案】B
【解析】
①把M、N的坐标代入解析式得到两个三元一次方程,两个方程相加即可求得a+c=0,②令y=0,求出△,判断图象与x轴的交点个数,设函数图象与x轴的两交点为x1,x2,求出|x1﹣x2|进行判断.③求出对称轴,然后结合a的取值范围判断,④根据m+n<0,![]() >0,即可判断,⑤根据交点坐标与系数的关系可以判断.
>0,即可判断,⑤根据交点坐标与系数的关系可以判断.
∵二次函数y=ax2+bx+c(a>0)经过点M(﹣1,2)和点N(1,﹣2),∴![]() ,∴①+②得:a+c=0;故①正确;
,∴①+②得:a+c=0;故①正确;
∵a=﹣c,∴b2﹣4ac>0,∴无论a取何值,此二次函数图象与x轴必有两个交点.
∵|x1﹣x2|=![]() =
=![]() =﹣1,∴
=﹣1,∴![]() >2,故②正确;
>2,故②正确;
二次函数y=ax2+bx+c(a>0)的对称轴x=﹣![]() =
=![]() ,当a>0时不能判定x<
,当a>0时不能判定x<![]() 时,y随x的增大而减小;故③错误;
时,y随x的增大而减小;故③错误;
∵﹣1<m<n<0,a>0,∴m+n<0,![]() >0,∴m+n<
>0,∴m+n<![]() ;故正确;
;故正确;
∵a=1,∴二次函数为y=x2+bx+c,∴OC2=c2=|x1x2|=OAOB,故正确.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示是二次函数
 图象的一部分,图象过点
图象的一部分,图象过点 ,二次函数图象对称轴为直线
,二次函数图象对称轴为直线 ,给出五个结论:①
,给出五个结论:① ;②
;② ;③当
;③当 时,
时, 随
随 的增大而增大;④方程
的增大而增大;④方程 的根为
的根为 ,
, ;⑤
;⑤ 其中正确结论是( )
其中正确结论是( )
A. ①②③ B. ①③④ C. ②③④ D. ③④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A(2,4),B(4,2),在x轴上取一点P,使点P到点A和点B的距离之和最小,则点P的坐标是_________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 、
、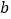 是两个任意独立的一位正整数,则点
是两个任意独立的一位正整数,则点 在抛物线
在抛物线 的上方的概率是( )
的上方的概率是( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】当三角形中一个内角
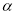 是另一个内角
是另一个内角 的2倍时,则称此三角形为“倍角三角形”,其中角
的2倍时,则称此三角形为“倍角三角形”,其中角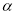 称为“倍角”.若“倍角三角形”中有一个内角为36°,则这个“倍角三角形”的“倍角”的度数可以是________________.
称为“倍角”.若“倍角三角形”中有一个内角为36°,则这个“倍角三角形”的“倍角”的度数可以是________________. -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+c的顶点为D(–1,2),与x轴的一个交点A在点(–3,0)和(–2,0)之间,其部分图象如下图,则以下结论:①b2–4ac<0;②a+b+c<0;③c–a=2;④方程ax2+bx+c–2=0有两个相等的实数根.其中正确结论的个数为( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】把大小和形状完全相同的
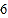 张卡片分成两组,每组
张卡片分成两组,每组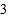 张,分别标上
张,分别标上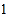 、
、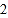 、
、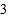 ,将这两组卡片分别放入两个盒子中搅匀,再从中随机抽取一张.
,将这两组卡片分别放入两个盒子中搅匀,再从中随机抽取一张. 请用画树状图的方法求取出的两张卡片数字之和为奇数的概率;
请用画树状图的方法求取出的两张卡片数字之和为奇数的概率; 若取出的两张卡片数字之和为奇数,则甲胜;取出的两张卡片数字之和为偶数,则乙胜;试分析这个游戏是否公平?请说明理由.
若取出的两张卡片数字之和为奇数,则甲胜;取出的两张卡片数字之和为偶数,则乙胜;试分析这个游戏是否公平?请说明理由.
相关试题

