【题目】如图,在平面直角坐标系中,点A(2,4),B(4,2),在x轴上取一点P,使点P到点A和点B的距离之和最小,则点P的坐标是_________.

参考答案:
【答案】(2,0)
【解析】
作A关于x轴的对称点C,连接AC交x轴于D,连接BC交交x轴于P,连接AP,此时点P到点A和点B的距离之和最小,求出C(的坐标,设直线CB的解析式是y=kx+b,把C、B的坐标代入求出解析式是y=x2,把y=0代入求出x即可.
作A关于x轴的对称点C,连接AC交x轴于D,连接BC交交x轴于P,连接AP,
则此时AP+PB最小,
即此时点P到点A和点B的距离之和最小,
∵A(2,4),
∴C(2,4),
设直线CB的解析式是y=kx+b,
把C、B的坐标代入得:
![]() ,
,
解得:k=1,b=2,
∴y=x2,
把y=0代入得:0=x2,
x=2,
即P的坐标是(2,0),

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,O是坐标原点,长方形OACB的顶点A、B分别在x轴与y轴上,已知OA=6,OB=10.点D为y轴上一点,其坐标为(0,2),点P从点A出发以每秒2个单位的速度沿线段AC﹣CB的方向运动,当点P与点B重合时停止运动,运动时间为t秒.
(1)当点P经过点C时,求直线DP的函数解析式;
(2)①求△OPD的面积S关于t的函数解析式;
②如图②,把长方形沿着OP折叠,点B的对应点B′恰好落在AC边上,求点P的坐标.
(3)点P在运动过程中是否存在使△BDP为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.



-
科目: 来源: 题型:
查看答案和解析>>【题目】有四根长度分别为3,4,5,x(x为正整数)的木棒,从中任取三根,首尾顺次相接都能组成一个三角形则组成的三角形的周长( )
A.最小值是11B.最小值是12C.最大值是14D.最大值是15
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示是二次函数
 图象的一部分,图象过点
图象的一部分,图象过点 ,二次函数图象对称轴为直线
,二次函数图象对称轴为直线 ,给出五个结论:①
,给出五个结论:① ;②
;② ;③当
;③当 时,
时, 随
随 的增大而增大;④方程
的增大而增大;④方程 的根为
的根为 ,
, ;⑤
;⑤ 其中正确结论是( )
其中正确结论是( )
A. ①②③ B. ①③④ C. ②③④ D. ③④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 、
、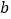 是两个任意独立的一位正整数,则点
是两个任意独立的一位正整数,则点 在抛物线
在抛物线 的上方的概率是( )
的上方的概率是( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 经过点
经过点 和点
和点 ,交
,交 轴于
轴于 ,
, 两点,交
两点,交 轴于
轴于 ,则:①
,则:① ;②无论
;②无论 取何值,此二次函数图象与
取何值,此二次函数图象与 轴必有两个交点,函数图象截
轴必有两个交点,函数图象截 轴所得的线段长度必大于
轴所得的线段长度必大于 ;③当函数在
;③当函数在 时,
时, 随
随 的增大而减小;④当
的增大而减小;④当 时,
时, ;⑤若
;⑤若 ,则
,则 .以上说法正确的有( )
.以上说法正确的有( )A. ①②③④⑤ B. ①②④⑤ C. ②③④ D. ①②③⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】当三角形中一个内角
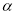 是另一个内角
是另一个内角 的2倍时,则称此三角形为“倍角三角形”,其中角
的2倍时,则称此三角形为“倍角三角形”,其中角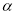 称为“倍角”.若“倍角三角形”中有一个内角为36°,则这个“倍角三角形”的“倍角”的度数可以是________________.
称为“倍角”.若“倍角三角形”中有一个内角为36°,则这个“倍角三角形”的“倍角”的度数可以是________________.
相关试题

