【题目】阅读下面的材料:
如图①,若线段AB在数轴上,A,B点表示的数分别为a,b(b>a),则线段AB的长(点A到点B的距离)可表示为AB=b﹣a

请用上面材料中的知识解答下面的问题:
如图②,一个点从数轴上的原点开始,先向左移动1cm到达A点,再向左移动2cm到达B点,然后向右移动7cm到达C点,用1个单位长度表示1cm
(1)请你在数轴上表示出A,B,C三点的位置,并直接写出线段AC的长度;
(2)若数轴上有一点D,且AD=4cm,则点D表示的数是什么?
(3)若将点A向右移动xcm,请用代数式表示移动后的点表示的数?
(4)若点B以每秒2cm的速度向左移动至点P1,同时点A,点C分别以每秒1cm和4cm的速度向右移动至点P2,点P3,设移动时间为t秒,试探索:P3P2﹣P1P2的值是否会随着t的变化而变化?请说明理由.
参考答案:
【答案】(1)数轴见解析;AC=5cm;(2)﹣5或3;(3)﹣1+x;(4)P3P2﹣P1P2的值不会随着t的变化而变化.
【解析】
(1)根据题意易画出图形,再由C点所表示的数减去A点所表示的数即可;
(2)设D表示的数为a,由绝对值的意义可求解;
(3)向右移动xcm,即A点所表示的数再加上xcm;
(4)用代数式表示出P3P2和P1P2,再相减即可得出结论.
解:(1)如图所示:
![]()
CA=4﹣(﹣1)=4+1=5(cm);
(2)设D表示的数为a,
∵AD=4,
∴|﹣1﹣a|=4,
解得:a=﹣5或3,
∴点D表示的数为﹣5或3;
(3)将点A向右移动xcm,则移动后的点表示的数为﹣1+x;
(4)P3P2﹣P1P2的值不会随着t的变化而变化,理由如下:
根据题意得:P3P2=(4+4t)﹣(﹣1+t)=5+3t,
P1P2=(﹣1+t)﹣(﹣3﹣2t)=2+3t,
∴P3P2﹣P1P2=(5+3t)﹣(2+3t)=3,
∴P3P2﹣P1P2的值不会随着t的变化而变化.
-
科目: 来源: 题型:
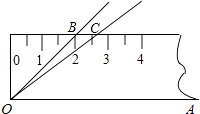
查看答案和解析>>【题目】如图,将45°的∠AOB按下面的方式放置在一把刻度尺上:顶点O与尺下沿的端点重合,OA与尺下沿重合,OB与尺上沿的交点B在尺上的读数恰为2cm.若按相同的方式将37°的∠AOC放置在该刻度尺上,则OC与尺上沿的交点C在尺上的读数约为cm.(结果精确到0.1cm,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过y轴上一点P(0,1)作平行于x轴的直线PB,分别交函数y1=x2(x≥0)与y2=
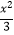 (x≥0)的图象于A1 , B1两点,过点B1作y轴的平行线交y1的图象于点A2 , 再过A2作直线A2B2∥x轴,交y2的图象于点B2 , 依次进行下去,连接A1A2 , B1B2 , A2A3 , B2B3 , …,记△A2A1B1的面积为S1 , △A2B1B2的面积为S2 , △A3A2B2的面积为S3 , △A3B2B3的面积为S4 , …则S2016=
(x≥0)的图象于A1 , B1两点,过点B1作y轴的平行线交y1的图象于点A2 , 再过A2作直线A2B2∥x轴,交y2的图象于点B2 , 依次进行下去,连接A1A2 , B1B2 , A2A3 , B2B3 , …,记△A2A1B1的面积为S1 , △A2B1B2的面积为S2 , △A3A2B2的面积为S3 , △A3B2B3的面积为S4 , …则S2016= 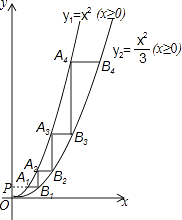
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,DE∥FG∥BC,AD:DF:FB=1:2:3,求S四边形DFGE:S四边形FBCG的值.
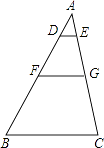
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,PB切⊙O于点B,联结PO并延长交⊙O于点E,过点B作BA⊥PE交⊙O于点A,联结AP,AE.

(1)求证:PA是⊙O的切线;
(2)如果OD=3,tan∠AEP= ,求⊙O的半径.
,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程中,解是x=﹣
 的是( )
的是( )A. 3(x-
 )=0 B. 2x﹣(x+1)=0 C.
)=0 B. 2x﹣(x+1)=0 C.  D.
D. 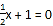
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:
 ,其中x的值从不等式组
,其中x的值从不等式组 的整数解中选取.
的整数解中选取.
相关试题

