【题目】如图,抛物线y=ax2+bx+c与x轴交于两点A(﹣4,0)和B(1,0),与y轴交于点C(0,2),动点D沿△ABC的边AB以每秒2个单位长度的速度由起点A向终点B运动,过点D作x轴的垂线,交△ABC的另一边于点E,将△ADE沿DE折叠,使点A落在点F处,设点D的运动时间为t秒.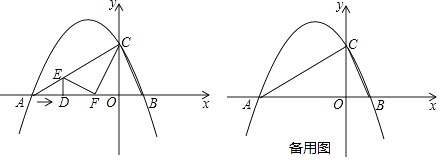
(1)求抛物线的解析式和对称轴;
(2)是否存在某一时刻t,使得△EFC为直角三角形?若存在,求出t的值;若不存在,请说明理由;
(3)设四边形DECO的面积为s,求s关于t的函数表达式.
参考答案:
【答案】
(1)解:把A(﹣4,0),B(1,0),点C(0,2)代入y=ax2+bx+c得, 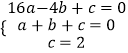 ,
,
∴ 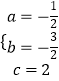 ,
,
∴抛物线的解析式为:y=﹣ ![]() x2﹣
x2﹣ ![]() bx+2,
bx+2,
对称轴为:直线x=﹣ ![]() ;
;
(2)解:存在,
∵AD=2t,
∴DF=AD=2t,
∴OF=4﹣4t,
∴D(2t﹣4,0),
∵直线AC的解析式为:y= ![]() x+2,
x+2,
∴E(2t﹣4,t),
∵△EFC为直角三角形,
①当∠EFC=90°,则△DEF∽△OFC,
∴ ![]() ,即
,即 ![]() =
= ![]() ,
,
解得:t= ![]() ,
,
②当∠FEC=90°,
∴∠AEF=90°,
∴△AEF是等腰直角三角形,
∴DE= ![]() AF,即t=2t,
AF,即t=2t,
∴t=0,(舍去),
③当∠ACF=90°,
则AC2+CF2=AF2,即(42+22)+[22+(4t﹣4)2]=(4t)2,
解得:t= ![]() ,
,
∴存在某一时刻t,使得△EFC为直角三角形,此时,t= ![]() 或
或 ![]() ;
;
(3)解:∵B(1,0),C(0,2),
∴直线BC的解析式为:y=﹣2x+2,
当D在y轴的左侧时,S= ![]() (DE+OC)OD=
(DE+OC)OD= ![]() (t+2)(4﹣2t)=﹣t2+4 (0<t<2),
(t+2)(4﹣2t)=﹣t2+4 (0<t<2),
当D在y轴的右侧时,如图2,
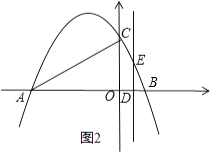
∵OD=4t﹣4,DE=﹣8t+10,
S= ![]() (DE+OC)OD=
(DE+OC)OD= ![]() (﹣8t+10+2)(4t﹣4)=﹣16t2+40t﹣24 (2<t<
(﹣8t+10+2)(4t﹣4)=﹣16t2+40t﹣24 (2<t< ![]() ).
).
【解析】(1)利用待定系数法把A、B坐标代入解析式即可;(2)△EFC为直角三角形时须分类讨论:①∠EFC=90°②∠FEC=90°,③∠ACF=90°三种情况讨论;(3)四边形DECO 的位置以y 轴为分界线,进行分类讨论:D在y轴的左侧与D在y轴的右侧,OD的表达式发生变化,须分类讨论.
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】去冬今春,某市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某乡中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件.
(1)求饮用水和蔬菜各有多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该乡中小学.已知每辆甲种货车最多可装饮用水40件和蔬菜10件,每辆乙种货车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD∥EF,BC∥AD,AC平分∠BAD,且与EF交于点O,那么与∠AOE相等的角有( )
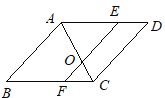
A. 6个B. 5个C. 4个D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,以BC为直径的⊙O交AB于点D,E是AC的中点,OE交CD于点F.
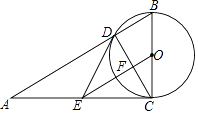
(1)若∠BCD=36°,BC=10,求BD的长;
(2)判断直线DE与⊙O的位置关系,并说明理由;
(3)求证:2CE2=ABEF. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠A=90°,AD∥BC,E为AB的中点,连接CE,BD,过点E作FE⊥CE于点E,交AD于点F,连接CF,已知2AD=AB=BC.

(1)求证:CE=BD;
(2)若AB=4,求AF的长度;
(3)求sin∠EFC的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个三角形的三边长分别为5、7、8,则其内切圆的半径为( )
A.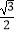
B.
C.
D.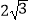
-
科目: 来源: 题型:
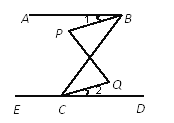
查看答案和解析>>【题目】如图,已知∠ABC=63°,∠ECB=117°.
(1) AB与ED平行吗?为什么?
(2)若∠P=∠Q,则∠1与∠2是否相等?说说你的理由.
相关试题

