搜索
【题目】已知一个三角形的三边长分别为5、7、8，则其内切圆的半径为（ ）
A.
B.
C.
D.
参考答案：
【答案】C
【解析】如图，AB=7，BC=5，AC=8，内切圆的半径为r，切点为D、E、F，作AD⊥BC于D，设BD=x，则CD=5﹣x．
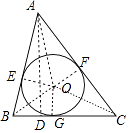
由勾股定理可知：AD2=AB2﹣BD2=AC2﹣CD2，
即72﹣x2=82﹣（5﹣x）2，解得x=1，
∴AD=4 
，
∵ 
BCAD= （AB+BC+AC）r，
×5×4 = ×20×r，
∴r= ，
故答案为：C
面积法求内切圆半径：先利用勾股定理列出方程求BC边上的高，进而求出三角形面积，三角形的面积还可以等于三个以O为顶点，各边为边的小三角形的面积和，从而建立以r 为未知数的简单的方程，求出r.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠ACB=90°，以BC为直径的⊙O交AB于点D，E是AC的中点，OE交CD于点F．
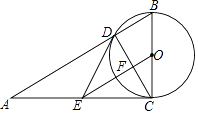
（1）若∠BCD=36°，BC=10，求BD的长；
（2）判断直线DE与⊙O的位置关系，并说明理由；
（3）求证：2CE2=ABEF． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=ax2+bx+c与x轴交于两点A（﹣4，0）和B（1，0），与y轴交于点C（0，2），动点D沿△ABC的边AB以每秒2个单位长度的速度由起点A向终点B运动，过点D作x轴的垂线，交△ABC的另一边于点E，将△ADE沿DE折叠，使点A落在点F处，设点D的运动时间为t秒．
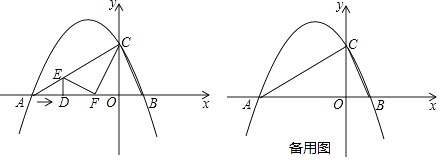
（1）求抛物线的解析式和对称轴；
（2）是否存在某一时刻t，使得△EFC为直角三角形？若存在，求出t的值；若不存在，请说明理由；
（3）设四边形DECO的面积为s，求s关于t的函数表达式． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，∠A=90°，AD∥BC，E为AB的中点，连接CE，BD，过点E作FE⊥CE于点E，交AD于点F，连接CF，已知2AD=AB=BC．
（1）求证：CE=BD；
（2）若AB=4，求AF的长度；
（3）求sin∠EFC的值． -
科目： 来源： 题型：
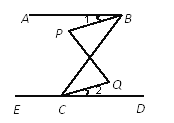
查看答案和解析>>【题目】如图，已知∠ABC=63°，∠ECB=117°.
(1) AB与ED平行吗？为什么？
(2)若∠P=∠Q，则∠1与∠2是否相等？说说你的理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两种商品原来的单价和为100元．因市场变化，甲商品降价10%，乙商品提价40%，调价后两种商品的单价和比原来的单价和提高了20%．甲、乙两种商品原来的单价各是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB=AC=2
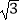，∠BAC=120°，点D，E都在边BC上，∠DAE=60°．若BD=2CE，则DE的长为 ．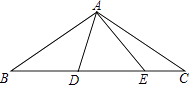 
相关试题
