搜索
【题目】解方程组：（1）
（用代入消元法）；（2）
（用加减消元法）
参考答案：
【答案】（1）
；（2）
.
【解析】
（1）规定用代入消元法，选择①中两个未知数，用一个未知数来表示另一个未知数x＝4＋y，代入②中求出y＝
，最后将y的值代回①中求出x＝
，即可求原方程组的解；
（2）规定用加减消元法，观察方程组消去其中的一个未知数y，只需将①×2②，可得x＝2，将x＝2代回原方程组中的②得y＝1，即可求出原方程组的解．
解：（1）
，
由①得：x＝4+y，③，
把③代入②得：4（4+y）+2y＝﹣1，
解得：y＝；
把y＝代入①得：x＝，
∴二元一次方程组的解为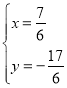
；
（2）
，
由①×2﹣②得：15x＝30，
解得：x＝2，
把x＝2代入②得：3×2+4y＝10，
解得：y＝1，
∴二元一次方程组的解为.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一副三角板
和
拼合在一起，边
与
重合，
，
，
，
．当点
从点
出发沿向下滑动时，点
同时从点
出发沿射线
向右滑动．当点从点滑动到点时，连接
，则
的面积最大值为_______
．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在菱形
中，
，
，点
是
边的中点，点
是
边上一动点（不与点
重合），延长
交射线
于点
，连接
，
．
（1）求证：四边形
是平行四边形；（2）填空：
①当
的值为_______时，四边形是矩形；②当
的值为______时，四边形是菱形． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在一个单位面积为1的方格纸上，△A1A2A3，△A3A4A5，△A5A6A7，……是斜边在x轴上，且斜边长分别为2，4，6，……的等腰直角三角形．若△A1A2A3的顶点坐标分别为A1（2，0），A2（1，-1），A3（0，0），则依图中所示规律，点A2019的横坐标为（ ）
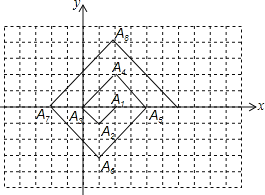
A. 1010B.
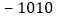C. 1008D.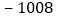 
-
科目： 来源： 题型：
查看答案和解析>>【题目】“中华人民共和国道路交通管理条例”规定：小汽车在城街路上行驶速度不得超过70千米
小时，如图，一辆小汽车在一条城市街路上直道行驶，某一时刻刚好行驶到路面对车速检测仪A的正前方60米处的C点，过了5秒后，测得小汽车所在的B点与车速检测仪A之间的距离为100米．
求BC间的距离；
这辆小汽车超速了吗？请说明理由．
【答案】这辆小汽车没有超速．
【解析】
（1）根据勾股定理求出BC的长；
（2）直接求出小汽车的时速，进行比较得出答案．(1)在Rt△ABC中，AC＝60 m，
AB＝100 m，且AB为斜边，根据勾股定理，得BC＝80 m.
(2)这辆小汽车没有超速．
理由：∵80÷5＝16(m/s)，
而16 m/s＝57.6 km/h，57.6<70，
∴这辆小汽车没有超速．
【点睛】
考查勾股定理的应用，熟练掌握勾股定理是解题的关键.
【题型】解答题
【结束】
19【题目】已知：如图，线段AC和BD相交于点G，连接AB，CD，E是CD上一点，F是DG上一点，
，且
．求证：
；若
，
，求
的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图（1）是某河上一座古拱桥的截面图，拱桥桥洞上沿是抛物线形状，抛物线两端点与水面的距离都是1m，拱桥的跨度为10m，桥洞与水面的最大距离是5m，桥洞两侧壁上各有一盏距离水面4m的景观灯．现把拱桥的截面图放在平面直角坐标系中，如图（2）．
求（1）抛物线的解析式；
（2）两盏景观灯P1、P2之间的水平距离.
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读材料，请回答下列问题．
材料一：我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”，即已知三角形的三边长，求它的面积，用现代式子表示即为：
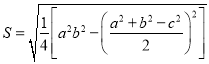①（其中
为三角形的三边长，
为面积），而另一个文明古国古希腊也有求三角形面积的“海伦公式”；
……②（其中
）材料二：对于平方差公式：
公式逆用可得：
，例：
（1）若已知三角形的三边长分别为4，5，7，请分别运用公式①和公式②，计算该三角形的面积；
（2）你能否由公式①推导出公式②？请试试，写出推导过程．
相关试题
