【题目】阅读材料,请回答下列问题.
材料一:我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”,即已知三角形的三边长,求它的面积,用现代式子表示即为: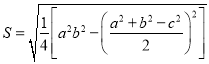 ①(其中
①(其中![]() 为三角形的三边长,
为三角形的三边长,![]() 为面积),而另一个文明古国古希腊也有求三角形面积的“海伦公式”;
为面积),而另一个文明古国古希腊也有求三角形面积的“海伦公式”;![]() ……②(其中
……②(其中![]() )
)
材料二:对于平方差公式:![]() 公式逆用可得:
公式逆用可得:![]() ,例:
,例:![]()
(1)若已知三角形的三边长分别为4,5,7,请分别运用公式①和公式②,计算该三角形的面积;
(2)你能否由公式①推导出公式②?请试试,写出推导过程.
参考答案:
【答案】(1)过程见解析,![]() ;(2)可以,见解析
;(2)可以,见解析
【解析】
(1)根据公式计算即可得出答案;
(2)根据完全平方公式和平方差公式推导即可得出答案.
解:(1)由公式①得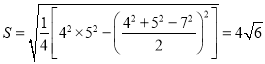
由②得![]() ,故
,故![]() .
.
(2)可以,过程如下:
由平方差公式,①中根号内的式子可化为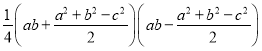
通分,得![]()
由完全平方公式,得![]()
由平方差公式,得![]() ③
③
由![]() ,得
,得![]()
代入③,得![]()
所以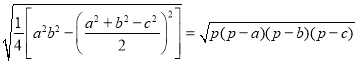
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程组:(1)
 (用代入消元法);(2)
(用代入消元法);(2)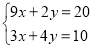 (用加减消元法)
(用加减消元法) -
科目: 来源: 题型:
查看答案和解析>>【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70千米
 小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪A的正前方60米处的C点,过了5秒后,测得小汽车所在的B点与车速检测仪A之间的距离为100米.
小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪A的正前方60米处的C点,过了5秒后,测得小汽车所在的B点与车速检测仪A之间的距离为100米. 求BC间的距离;
求BC间的距离; 这辆小汽车超速了吗?请说明理由.
这辆小汽车超速了吗?请说明理由.
【答案】这辆小汽车没有超速.
【解析】
(1)根据勾股定理求出BC的长;
(2)直接求出小汽车的时速,进行比较得出答案.(1)在Rt△ABC中,AC=60 m,
AB=100 m,且AB为斜边,根据勾股定理,得BC=80 m.
(2)这辆小汽车没有超速.
理由:∵80÷5=16(m/s),
而16 m/s=57.6 km/h,57.6<70,
∴这辆小汽车没有超速.
【点睛】
考查勾股定理的应用,熟练掌握勾股定理是解题的关键.
【题型】解答题
【结束】
19【题目】已知:如图,线段AC和BD相交于点G,连接AB,CD,E是CD上一点,F是DG上一点,
 ,且
,且 .
. 求证:
求证: ;
; 若
若 ,
, ,求
,求 的度数.
的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1)是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯.现把拱桥的截面图放在平面直角坐标系中,如图(2).


求(1)抛物线的解析式;
(2)两盏景观灯P1、P2之间的水平距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】贺岁片《流浪地球》被称为开启了中国科幻片的大门,2019也被称为中国科幻片的元年.某电影院为了全面了解观众对《流浪地球》的满意度情况,进行随机抽样调查,分为四个类别:A.非常满意;B.满意;C.基本满意;D.不满意.依据调查数据绘制成图1和图2的统计图(不完整).根据以上信息,解答下列问题:

(1)本次接受调查的观众共有 人;
(2)扇形统计图中,扇形C的圆心角度数是 .
(3)请补全条形统计图;
(4)春节期间,该电影院来观看《流浪地球》的观众约3000人,请估计观众中对该电影满意(A、B、C类视为满意)的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了让学生能更加了解温州历史,某校组织七年级师生共480人参观温州博物馆.学校向租车公司租赁A、B两种车型接送师生往返,若租用A型车3辆,B型车6辆,则空余15个座位;若租用A型车5辆,B型车4辆,则15人没座位.
(1)求A、B两种车型各有多少个座位;
(2)若A型车日租金为350元,B型车日租金为400元,且租车公司最多能提供7辆B型车,应怎样租车能使座位恰好坐满且租金最少,并求出最少租金.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,地面上两个村庄C、D处于同一水平线上,一飞行器在空中以6千米/小时的速度沿MN方向水平飞行,航线MN与C、D在同一铅直平面内.当该飞行器飞行至村庄C的正上方A处时,测得∠NAD=60°;该飞行器从A处飞行40分钟至B处时,测得∠ABD=75°.求村庄C、D间的距离(
 取1.73,结果精确到0.1千米)
取1.73,结果精确到0.1千米)
相关试题

