搜索
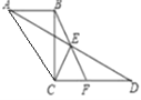
【题目】如图，AB∥CD，连接AD，点E是AD的中点，连接BE并延长交CD于F点．
(1)请说明△ABE≌△DFE的理由；
(2)连接CB，AC，若CB⊥CD，AC=CD，∠D=30°，CD=2，求BF的长．
参考答案：
【答案】（1）证明见解析；（2）BF=2
【解析】
利用三角形全等判定条件ASA进行判断.
利用30°所对直角边等于斜边的一半求出CE的长，再利用BF=2CE求出BF的长度.
证明：∵AB∥CD
∴∠BAE=∠EDF
∵点E是AD的中点
∴AE=ED
又∵∠AEB=∠FED
∴△ABE≌△DFE（ASA）
（2）∵AC=CD 且E为AD中点 ∴CE⊥AD
∵∠D=30°且CD=2 ∴CE=1
又∵CB⊥CD且BE=EF ∴BF=2CE
∴BF=2.
-
科目： 来源： 题型：
查看答案和解析>>【题目】将一批抗疫物资运往武汉，货主准备租用汽车运输公司的甲、乙两种货车，已知过去两次租用这两种货车的情况如下表：
甲种货车(辆)
乙种货车(辆)
总量(吨)
第一次
4
5
31
第二次
3
6
30
（1）甲、乙两种货车每辆分别能装货多少吨？
（2）现有45吨物资需要再次运往武汉，准备同时租用这两种货车，每辆均全部装满货物，问有哪几种租车方案？请全部设计出来．
-
科目： 来源： 题型：
查看答案和解析>>【题目】多好佳水果店在批发市场购买某种水果销售，第一次用1500元购进若干千克，并以每千克9元出售，很快售完．由于水果畅销，第二次购买时，每千克的进价比第一次提高了10%，用1694元所购买的水果比第一次多20千克，以每千克10元售出100千克后，因出现高温天气，水果不易保鲜，为减少损失，便降价45%售完剩余的水果．
(1)第一次水果的进价是每千克多少元？
(2)该水果店在这两次销售中，总体上是盈利还是亏损？盈利或亏损了多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】我市某校准备组织学生及学生家长坐高铁到杭州进行社会实践，为了便于管理．所有人员必须乘坐在同一列高铁上．根据报名人数，若都买一等座单程火车票需6560元，若都买二等座单程火车票，则需3120元（学生票二等座打7.5折，一等座不打折）．已知学生家长与教师的人数之比为3：1，余姚北站到杭州东站的火车票价格如表所示：
运行区间
票价
上车站
下车站
一等座
二等座
余姚北
杭州东
82（元）
48（元）
（1）参加社会实践的老师、家长与学生各有多少人？
（2）由于各种原因，二等座火车票单程只能买m张（m小于参加社会实践的人数），其余的须买一等座火车票，在保证每位参与人员都有座位坐的前提下，请你设计最经济的购票方案，并写出购买火车票的总费用（单程）y（元）（用含m的代数式表示）． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，已知
，
，其中
满足
．
（1）填空：
_______，
________；（2）若在第三象限内有一点
，用含
的式子表示
的面积；（3）在（2）条件下，当
时，点
是坐标轴上的动点，当满足
的面积是的面积的2倍时，求点的坐标． -
科目： 来源： 题型：
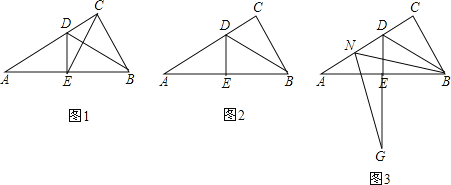
查看答案和解析>>【题目】在Rt△ABC中，∠ACB=90°，∠A=30°，BD是△ABC的角平分线，DE⊥AB于点E.
(1)如图1，连接EC，求证：△EBC是等边三角形；
(2)点M是线段CD上的一点(不与点C，D重合)，以BM为一边，在BM的下方作∠BMG=60°，MG交DE延长线于点G.求证：AD=DG+MD；
(3)点N是线段AD上的一点，以BN为一边，在BN的下方作∠BNG=60°，NG交DE延长线于点G.请在图3中画出图形，并直接写出ND，DG与AD数量之间的关系.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某种流感病毒，有一人患了这种流感，在每轮传染中一人将平均传给x人．
（1）求第一轮后患病的人数；（用含x的代数式表示）
（2）在进入第二轮传染之前，有两位患者被及时隔离并治愈，问第二轮传染后总共是否会有21人患病的情况发生，请说明理由．
相关试题
