【题目】某种流感病毒,有一人患了这种流感,在每轮传染中一人将平均传给x人.
(1)求第一轮后患病的人数;(用含x的代数式表示)
(2)在进入第二轮传染之前,有两位患者被及时隔离并治愈,问第二轮传染后总共是否会有21人患病的情况发生,请说明理由.
参考答案:
【答案】(1)(1+x)人,(2)21人.
【解析】试题分析: (1)设每轮传染中平均每人传染了x人.开始有一人患了流感,第一轮的传染源就是这个人,他传染了x人,则第一轮后共有(1+x)人患了流感;
(2)第二轮传染中,这些人中的每个人又传染了x人,因进入第二轮传染之前,有两位患者被及时隔离并治愈,则第二轮后共有x-1+x(x-1)人患了流感,而此时患流感人数为21,根据这个等量关系列出方程若能求得正整数解即可会有21人患病.
试题解析:
(1)(1+x)人,
(2)设在每轮传染中一人将平均传给x人,根据题意得:
x-1+x(x-1)=21
整理得:x2-1=21
解得: ![]()
∵![]() 都不是正整数,
都不是正整数,
∴第二轮传染后共会有21人患病的情况不会发生.
-
科目: 来源: 题型:
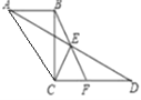
查看答案和解析>>【题目】如图,AB∥CD,连接AD,点E是AD的中点,连接BE并延长交CD于F点.
(1)请说明△ABE≌△DFE的理由;
(2)连接CB,AC,若CB⊥CD,AC=CD,∠D=30°,CD=2,求BF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知
 ,
, ,其中
,其中 满足
满足 .
.
(1)填空:
 _______,
_______, ________;
________;(2)若在第三象限内有一点
 ,用含
,用含 的式子表示
的式子表示 的面积;
的面积;(3)在(2)条件下,当
 时,点
时,点 是坐标轴上的动点,当满足
是坐标轴上的动点,当满足 的面积是
的面积是 的面积的2倍时,求点
的面积的2倍时,求点 的坐标.
的坐标. -
科目: 来源: 题型:
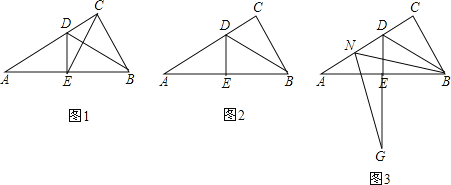
查看答案和解析>>【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于点E.
(1)如图1,连接EC,求证:△EBC是等边三角形;
(2)点M是线段CD上的一点(不与点C,D重合),以BM为一边,在BM的下方作∠BMG=60°,MG交DE延长线于点G.求证:AD=DG+MD;
(3)点N是线段AD上的一点,以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G.请在图3中画出图形,并直接写出ND,DG与AD数量之间的关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简再求值:当a=9时,求a+
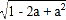 的值,甲乙两人的解答如下:
的值,甲乙两人的解答如下:甲的解答为:原式=a+
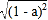 =a+(1-a)=1.
=a+(1-a)=1.乙的解答为:原式=a+
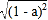 =a+(a-1)=2a-1=17.
=a+(a-1)=2a-1=17.两种解答中,_____的解答是错误的,错误的原因是当a=9时______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:圆心在三角形的一边上,与另一边相切,且经过三角形一个顶点(非切点)的圆,称为这个三角形圆心所在边上的“伴随圆”.

(1)如图1,△ABC中,∠C=90°,AB=5,BC=3,则AC边上的伴随圆的半径为 .
(2)如图2,已知等腰△ABC,AB=AC=5,BC=6,画草图并直接写出它的所有伴随圆的半径.
(3)如图3,△ABC中,∠ACB=90°,点P在边AB上,AP=2BP,D为AC中点,且∠CPD=90°.
①求证:△CPD的外接圆是△ABC某一条边上的伴随圆;
②求cos∠PDC的值.
相关试题

