【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F. 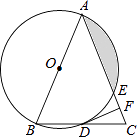
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.
参考答案:
【答案】
(1)证明:连接OD,
∵OB=OD,
∴∠ABC=∠ODB,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ODB=∠ACB,
∴OD∥AC,
∵DF是⊙O的切线,
∴DF⊥OD,
∴DF⊥AC
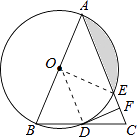
(2)解:连接OE,
∵DF⊥AC,∠CDF=22.5°,
∴∠ABC=∠ACB=67.5°,
∴∠BAC=45°,
∵OA=OE,
∴∠AOE=90°,
∵⊙O的半径为4,
∴S扇形AOE=4π,S△AOE=8 ,
∴S阴影=4π﹣8.

【解析】(1)连接OD,易得∠ABC=∠ODB,由AB=AC,易得∠ABC=∠ACB,等量代换得∠ODB=∠ACB,利用平行线的判定得OD∥AC,由切线的性质得DF⊥OD,得出结论;(2)连接OE,利用(1)的结论得∠ABC=∠ACB=67.5°,易得∠BAC=45°,得出∠AOE=90°,利用扇形的面积公式和三角形的面积公式得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有理数a,b,c在数轴上的对应点如图所示.

(1)在横线上填上“>”或“=”或“<”:
a 0,a-b 0,
 .
.(2)在数轴上标出表示有理数-a,-b,-c的点;
(3)用“>”把a,b,c,-a,-b,-c连接起来.
-
科目: 来源: 题型:
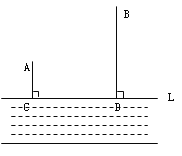
查看答案和解析>>【题目】如图,A、B两个小集镇在河流CD的同侧,分别到河的距离为AC=10千米,BD=30千米,且CD=30千米,现在要在河边建一自来水厂,向A、B两镇供水,铺设水管的费用为每千米3万,请你在河流CD上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某出租车以汽车站为出发点,在东西方向的城市道路上进行营运,若规定向东为正,向西为负,行车依先后顺序记录如下(单位:千米):
+4,-5,+9,-3,+6,-3,-8,-4,+7,-6.
(1)计算说明出租车将最后一名乘客送到目的地,此时离汽车站多远?在汽车站什么方向?
(2)若该出租车每千米收费标准为3元,求出租车的营业额是多少元?
-
科目: 来源: 题型:
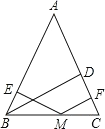
查看答案和解析>>【题目】大家在学完勾股定理的证明后发现运用“同一图形的面积不同表示方式相同”可 以证明一类含有线段的等式,这种解决问题的方法我们称之为面积法.学有所用:在等腰 三角形 ABC中,AB=AC,其一腰上的高为h,M 是底边BC上的任意一点,M 到腰AB、AC 的距离分别为 h1、h2 .
(1)请你结合图形来证明: h1+h2=h;
(2)当点M在BC延长线上时,h1、h2、h 之间又有什么样的结论.请你画出图形,并直
接写出结论不必证明;
(3)利用以上结论解答,如图在平面直角坐标系中有两条直线l1:y=x+3,l2:y=-3x+3
若 l2上的一点M 到l1的距离是
 ,求点 M 的坐标.
,求点 M 的坐标.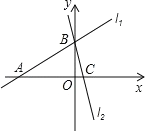
-
科目: 来源: 题型:
查看答案和解析>>【题目】把一张纸对折1次后,就得到2层;对折2次后,就得到4层;对折3次后,就得到8层;……,按照这样对折下去.
(1)求将一张纸对折6次后,层数是多少?
(2)求将一张纸对折n次后,层数是多少(用含n的式子表示)?
(3)若一张纸的厚度均为0.5mm,求将该纸张对折2018次后的总的厚度是多少mm?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,四边形ABCD、CEFG均为正方形.

(1)求证:BE=DG.
(2)如图②,四边形ABCD、CEFG均为菱形,且∠A=∠F.是否仍存在结论BE=DG,若不存在,请说明理由;若存在,给出证明.
(3)如图③,四边形ABCD、CEFG均为菱形,点E在边AD上,点G在AD延长线上.若AE=2ED,∠A=∠F,△EBC的面积为8,则菱形CEFG的面积为 .
相关试题

