【题目】如图①,四边形ABCD、CEFG均为正方形. 
(1)求证:BE=DG.
(2)如图②,四边形ABCD、CEFG均为菱形,且∠A=∠F.是否仍存在结论BE=DG,若不存在,请说明理由;若存在,给出证明. 
(3)如图③,四边形ABCD、CEFG均为菱形,点E在边AD上,点G在AD延长线上.若AE=2ED,∠A=∠F,△EBC的面积为8,则菱形CEFG的面积为 . 
参考答案:
【答案】
(1)证明:∵四边形ABCD、四边形CEFG均为正方形,
∴BC=CD,CE=CG,
∵∠BCD=∠ECG=90°,
∴∠BCD﹣∠ECD=∠ECG﹣∠ECD,
即∠BCE=∠DCG,
在△BCE和△DCG中,
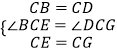 ,
,
∴△BCE≌△DCG,
∴BE=DG
(2)解:存在
理由:∵四边形ABCD、四边形CEFG均为菱形,
∴BC=CD,CE=CG,∠BCD=∠A,∠ECG=∠F,
∵∠A=∠F,
∴∠BCD=∠ECG,
∴∠BCD﹣∠ECD=∠ECG﹣∠ECD,
即∠BCE=∠DCG,
∴△BCE≌△DCG.,
∴BE=DG
(3)![]()
【解析】解:(3)∵四边形ABCD是菱形,S△EBC=8, ∴S△AEB+S△EDC=8,
∵AE=2DE,
∴S△AEB=2S△EDC ,
∴S△EDC= ![]() ,
,
∵△BCE≌△DCG,
∴S△DGC=S△EBC=8,
∴S△ECG=8+ ![]() =
= ![]() ,
,
∴菱形CEFG的面积=2S△EGC= ![]() ,
,
所以答案是 ![]() .
.
【考点精析】通过灵活运用正方形的性质,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.
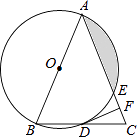
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】大家在学完勾股定理的证明后发现运用“同一图形的面积不同表示方式相同”可 以证明一类含有线段的等式,这种解决问题的方法我们称之为面积法.学有所用:在等腰 三角形 ABC中,AB=AC,其一腰上的高为h,M 是底边BC上的任意一点,M 到腰AB、AC 的距离分别为 h1、h2 .
(1)请你结合图形来证明: h1+h2=h;
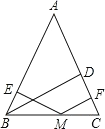
(2)当点M在BC延长线上时,h1、h2、h 之间又有什么样的结论.请你画出图形,并直
接写出结论不必证明;
(3)利用以上结论解答,如图在平面直角坐标系中有两条直线l1:y=x+3,l2:y=-3x+3
若 l2上的一点M 到l1的距离是
 ,求点 M 的坐标.
,求点 M 的坐标.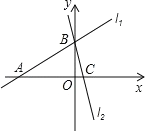
-
科目: 来源: 题型:
查看答案和解析>>【题目】把一张纸对折1次后,就得到2层;对折2次后,就得到4层;对折3次后,就得到8层;……,按照这样对折下去.
(1)求将一张纸对折6次后,层数是多少?
(2)求将一张纸对折n次后,层数是多少(用含n的式子表示)?
(3)若一张纸的厚度均为0.5mm,求将该纸张对折2018次后的总的厚度是多少mm?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx﹣3的图象与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C.该抛物线的顶点为M.
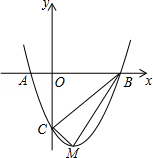
(1)求该抛物线的解析式;
(2)判断△BCM的形状,并说明理由.
(3)探究坐标轴上是否存在点P,使得以点P,A,C为顶点的三角形与△BCM相似?若存在,请求出点P的坐标,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车间同时开始加工一批零件,从开始加工到加工完这批零件,甲车间工作了9小时,乙车间在中途停工一段时间维修设备,修好后马上按停工前的工作效率继续加工,直到与甲车间同时完成这批零件的加工任务为止,设甲、乙两车间各自加工零件的数量为y(个),甲车间加工的时间为x(时),y与x之间的函数图象如图所示,下列说法其中正确的个数为( )
①这批零件的总个数为1260个;
②甲车间每小时加工零件个数为80个;
③乙车间维修设备后,乙车间加工零件数量y与x之间的函数关系式y=60x﹣120;
④乙车间维修设备用了2个小时
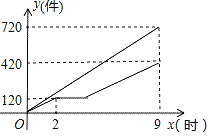
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个菱形两条对角线长的和是10,菱形的面积是12,则菱形的边长为_____.
相关试题

