搜索
【题目】如图，平面直角坐标系中，直线AB：y=﹣x+b交y轴于点A，交x轴于点B，S△AOB=8．
（1）求点B的坐标和直线AB的函数表达式；
（2）直线a垂直平分OB交AB于点D，交x轴于点E，点P是直线a上一动点，且在点D的上方，设点P的纵坐标为m．
①用含m的代数式表示△ABP的面积；
②当S△ABP=6时，求点P的坐标.
参考答案：
【答案】（1）
，
；（2）①
，②
【解析】
（1）可求得直线
与两轴相交的两点的坐标为
，即
，由
可求得
的值，继而求得点
的坐标和直线的解析式；
（2）①由题知直线
垂直平分
可知
，将
代入直线
的解析式可求得点
的坐标，设点
的坐标为
，然后依据
可得到
的面积与
的函数关系式；②由
得到关于的方程可求得的值，从而得到点的坐标；
(1)直线与两轴相交的两点的坐标为，即，
解得
∴点的坐标为
直线的函数表达式：
（2）①∵垂直平分，
∴．
∵将代入得：
．
∴点的坐标为
．
∵点的坐标为(
，
∴
．
∵，
∴
．
②∵，
∴
，解得：
．
∴点的坐标为
．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了弘扬优秀传统文化，某校组织了一次“诗词大会”，小明和小丽同时参加，其中，有一道必答题是：从如图所示的九宫格中选取七个字组成一句唐诗，其答案为“两个黄鹂鸣翠柳”．
(1)小明回答该问题时，对第二个字是选“个”还是选“只”难以抉择，若随机选择其中一个，则小明回答正确的概率是__________；
(2)小丽回答该问题时，对第二个字是选“个”还是选“只”、第五个字是选“鸣”还是选“明”都难以抉择，若分别随机选择，请用列表或画树状图的方法求小丽回答正确的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数y＝（m+1）x+
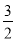的图象与x轴的负半轴相交于点A，与y轴相交于点B，且△OAB的面积为
．
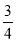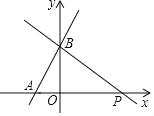
（1）求m的值及点A的坐标；
（2）过点B作直线BP与x轴的正半轴相交于点P，且OP＝3OA，求直线BP的解析式．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某地城管需要从甲、乙两个仓库向A、B两地分别运送10吨和5吨的防寒物资，甲、乙两仓库分别有8吨、7吨防寒物资．从甲、乙两仓库运送防寒物资到A、B两地的运费单价（元/吨）如表1，设从甲仓库运送到A地的防寒物资为x吨（如表2）．
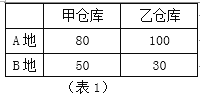
（1）完成表2 , ；
（2）求运送的总运费y（元）与x（吨）之间的函数表达式，并直接写出x的取值范围；
（3）直接写出最低总运费．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一枚运载火箭从距雷达站C处5km的地面O处发射，当火箭到达点A，B时，在雷达站C处测得点A，B的仰角分别为34°，45°，其中点O，A，B在同一条直线上．求A，B两点间的距离（结果精确到0.1km）．
（参考数据：sin34°=0.56，cos34°=0.83，tan34°=0.67．）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图是甲、乙两家运输公司规定每位旅客携带行李的费用与所带行李质量之间的关系图．
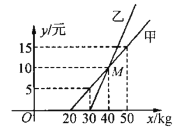
（1）由图可知，行李质量只要不超过______kg，甲公司就可免费携带，如果超过了规定的质量，则每超过1 kg要付运费_______元；
（2）若设旅客携带的行李质量为x(kg)，所付的行李费是y（元），请分别写出y甲与y乙（元）随x(kg)之间变化的关系式；
（3）若你准备携带45 kg的行李出行，在甲、乙两家公司中你会选择哪一家？应付行李费多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线l：y=
x+6交x、y轴分别为A、B两点，C点与A点关于y轴对称．动点P、Q分别在线段AC、AB上（点P不与点A、C重合），满足∠BPQ=∠BAO．
（1）点A坐标是 ，点B的坐标 ，BC= ．
（2）当点P在什么位置时，△APQ≌△CBP，说明理由．
（3）当△PQB为等腰三角形时，求点P的坐标．
相关试题
