【题目】如图,直线l:y=![]() x+6交x、y轴分别为A、B两点,C点与A点关于y轴对称.动点P、Q分别在线段AC、AB上(点P不与点A、C重合),满足∠BPQ=∠BAO.
x+6交x、y轴分别为A、B两点,C点与A点关于y轴对称.动点P、Q分别在线段AC、AB上(点P不与点A、C重合),满足∠BPQ=∠BAO.

(1)点A坐标是 ,点B的坐标 ,BC= .
(2)当点P在什么位置时,△APQ≌△CBP,说明理由.
(3)当△PQB为等腰三角形时,求点P的坐标.
参考答案:
【答案】(1)A的坐标是(﹣8,0),点B的坐标是(0,6),BC=![]() =10,(2)当P的坐标是(2,0)时,△APQ≌△CBP.(3)(﹣8,0),(0,6),10.
=10,(2)当P的坐标是(2,0)时,△APQ≌△CBP.(3)(﹣8,0),(0,6),10.
【解析】
试题分析:(1)把x=0和y=0分别代入一次函数的解析式,求出A、B的坐标,根据勾股定理求出BC即可.
(2)求出∠PAQ=∠BCP,∠AQP=∠BPC,根据点的坐标求出AP=BC,根据全等三角形的判定推出即可.
(3)分为三种情况:①PQ=BP,②BQ=QP,③BQ=BP,根据(2)即可推出①,根据三角形外角性质即可判断②,根据勾股定理得出方程,即可求出③.
解:(1)∵y=![]() x+6
x+6
∴当x=0时,y=6,
当y=0时,x=﹣8,
即点A的坐标是(﹣8,0),点B的坐标是(0,6),
∵C点与A点关于y轴对称,
∴C的坐标是(8,0),
∴OA=8,OC=8,OB=6,
由勾股定理得:BC=![]() =10,
=10,
(2)当P的坐标是(2,0)时,△APQ≌△CBP,
理由是:∵OA=8,P(2,0),
∴AP=8+2=10=BP,
∵∠BPQ=∠BAO,∠BAO+∠AQP+∠APQ=180°,∠APQ+∠BPQ+∠BPC=180°,
∴∠AQP=∠BPC,
∵A和C关于y轴对称,
∴∠BAO=∠BCP,
在△APQ和△CBP中,
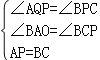 ,
,
∴△APQ≌△CBP(AAS),
∴当P的坐标是(2,0)时,△APQ≌△CBP.
(3)分为三种情况:
①当PB=PQ时,∵由(2)知,△APQ≌△CBP,
∴PB=PQ,
即此时P的坐标是(2,0);
②当BQ=BP时,则∠BPQ=∠BQP,
∵∠BAO=∠BPQ,
∴∠BAO=∠BQP,
而根据三角形的外角性质得:∠BQP>∠BAO,
∴此种情况不存在;
③当QB=QP时,则∠BPQ=∠QBP=∠BAO,
即BP=AP,
设此时P的坐标是(x,0),
∵在Rt△OBP中,由勾股定理得:BP2=OP2+OB2,
∴(x+8)2=x2+62,
解得:x=﹣![]() ,
,
即此时P的坐标是(﹣![]() ,0).
,0).
∴当△PQB为等腰三角形时,点P的坐标是(2,0)或(﹣![]() ,0).
,0).
故答案为:(﹣8,0),(0,6),10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,直线AB:y=﹣x+b交y轴于点A,交x轴于点B,S△AOB=8.

(1)求点B的坐标和直线AB的函数表达式;
(2)直线a垂直平分OB交AB于点D,交x轴于点E,点P是直线a上一动点,且在点D的上方,设点P的纵坐标为m.
①用含m的代数式表示△ABP的面积;
②当S△ABP=6时,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一枚运载火箭从距雷达站C处5km的地面O处发射,当火箭到达点A,B时,在雷达站C处测得点A,B的仰角分别为34°,45°,其中点O,A,B在同一条直线上.求A,B两点间的距离(结果精确到0.1km).
(参考数据:sin34°=0.56,cos34°=0.83,tan34°=0.67.)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是甲、乙两家运输公司规定每位旅客携带行李的费用与所带行李质量之间的关系图.
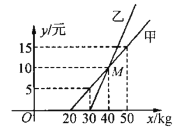
(1)由图可知,行李质量只要不超过______kg,甲公司就可免费携带,如果超过了规定的质量,则每超过1 kg要付运费_______元;
(2)若设旅客携带的行李质量为x(kg),所付的行李费是y(元),请分别写出y甲与y乙(元)随x(kg)之间变化的关系式;
(3)若你准备携带45 kg的行李出行,在甲、乙两家公司中你会选择哪一家?应付行李费多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在求1+3+32+34+35+36+37+38的值时,张红发现:从第二个加数起每一个加数都是前一个加数的3倍,于是她假设:S=1+3+32+33+34+35+36+37+38①,然后在①式的两边都乘以3,得:3S=3+32+33+34+35+36+37+38+39②,②﹣①得:3S﹣S=39﹣1,即2S=39﹣1,∴S=
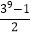 .
.请阅读张红发现的规律,并帮张红解决下列问题:
(1)爱动脑筋的张红想:如果把“3”换成字母m(m≠0且m≠1),应该能用类比的方法求出1+m+m2+m3+m4+…+m2018的值,对该式的值,你的猜想是______(用含m的代数式表示).
(2)证明你的猜想是正确的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,将坐标原点O沿x轴向左平移2个单位长度得到点A,过点A作y轴的平行线交反比例函数y=
 的图象于点B,AB=
的图象于点B,AB= .
.(1)求反比例函数的解析式;
(2)若P(x1,y1)、Q(x2,y2)是该反比例函数图象上的两点,且x1<x2时,y1>y2,指出点P、Q各位于哪个象限?并简要说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,O是边AC上一点,以O为圆心,OA为半径的圆分别交AB,AC于点E,D,在BC的延长线上取点F,使得BF=EF,EF与AC交于点G.
(1)试判断直线EF与⊙O的位置关系,并说明理由;
(2)若OA=2,∠A=30°,求图中阴影部分的面积.

相关试题

