搜索
【题目】如图，O为坐标原点，四边形OACB是菱形，OB在x轴的正半轴上，sin∠AOB= 
，反比例函数y= 
在第一象限内的图像经过点A，与BC交于点F，则△AOF的面积等于（ ） 
A.60
B.80
C.30
D.40
参考答案：
【答案】D
【解析】解：过点A作AM⊥x轴于点M，如图所示．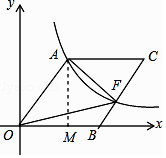 
设OA=a，
在Rt△OAM中，∠AMO=90°，OA=a，sin∠AOB= 
，
∴AM=OAsin∠AOB= a，OM= 
= 
a，
∴点A的坐标为（ a， a）．
∵点A在反比例函数y= 
的图像上，
∴ a× a= 
=48，
解得：a=10，或a=﹣10（舍去）．
∴AM=8，OM=6，OB=OA=10．
∵四边形OACB是菱形，点F在边BC上，
∴S△AOF= 
S菱形OBCA= OBAM=40．
故选D．
【考点精析】关于本题考查的菱形的性质，需要了解菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半才能得出正确答案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，点A、B、C、D是坐标轴上的点且点C坐标是（0，﹣1），AB=5，点（a，b）在如图所示的阴影部分内部（不包括边界），已知OA=OD=4，则a的取值范围是（ ）
A.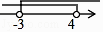
B.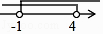
C.
D.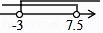
-
科目： 来源： 题型：
查看答案和解析>>【题目】用“*”定义一种新运算：对于任意有理数a和b，规定a*b=ab2+2ab+a．
如：1*3=1×32+2×1×3+1=16
（1）求2*（﹣2）的值；
（2）若2*x=m,
（其中x为有理数），试比较m，n的大小；（3）若[
]
=a+4，求a的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知，点E、F分别在直线AB，CD上，点P在AB、CD之间，连结EP、FP，如图1，过FP上的点G作GH∥EP，交CD于点H，且∠1=∠2．
（1）求证：AB∥CD；
（2）如图2，将射线FC沿FP折叠，交PE于点J，若JK平分∠EJF，且JK∥AB，则∠BEP与∠EPF之间有何数量关系，并证明你的结论；
（3）如图3，将射线FC沿FP折叠，将射线EA沿EP折叠，折叠后的两射线交于点M，当EM⊥FM时，求∠EPF的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一个正方体的六个面上分别标有1、2、3、4、5、6，根据图中从各个方向看到的数字，解答下面的问题：“？”处的数字是_____．
-
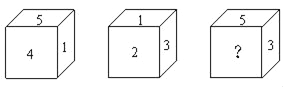
科目： 来源： 题型：
查看答案和解析>>【题目】先化简，再求值：
(1)(3a2－ab＋7)－(5ab－4a2＋7)，其中， a＝2，b＝
；(2)3(ab－5b2＋2a2)－(7ab＋16a2－25b2)，其中|a－1|＋(b＋1)2＝0.
-
科目： 来源： 题型：
查看答案和解析>>【题目】下面是王老师在数学课堂上给同学们出的一道数学题，要求对以下实数进行分类填空：
－
，0，
，
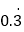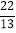，18，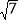
，
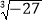，－0.56，3.14159，
，
，
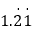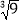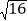，0.8080080008…，－
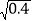.(1)有理数集合：________________________________________________________________________；
(2)无理数集合：________________________________________________________________________；
(3)非负整数集合：________________________________________________________________________；
(4)分数集合：________________________________________________________________________.
相关试题
