【题目】在平面直角坐标系中,点A、B、C、D是坐标轴上的点且点C坐标是(0,﹣1),AB=5,点(a,b)在如图所示的阴影部分内部(不包括边界),已知OA=OD=4,则a的取值范围是( ) 
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】D
【解析】解:∵AB=5,OA=4, ∴OB= ![]() =3,
=3,
∴点B(﹣3,0).
∵OA=OD=4,
∴点A(0,4),点D(4,0).
设直线AD的解析式为y=kx+b,
将A(0,4)、D(4,0)代入y=kx+b,![]() ,解得:
,解得: ![]() ,
,
∴直线AD的解析式为y=﹣x+4;
设直线BC的解析式为y=mx+n,
将B(﹣3,0)、C(0,﹣1)代入y=mx+n,![]() ,解得:
,解得: 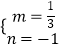 ,
,
∴直线BC的解析式为y=﹣ ![]() x﹣1.
x﹣1.
联立直线AD、BC的解析式成方程组, ,解得:
,解得: 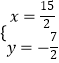 ,
,
∴直线AD、BC的交点坐标为( ![]() ,﹣
,﹣ ![]() ).
).
∵点(a,b)在如图所示的阴影部分内部(不包括边界),
∴﹣3<a< ![]() .
.
故选D.
根据勾股定理即可得出OB的长度,由此可得出点B的坐标,由OA、OD的长度可得出点A、D的坐标,根据点A、D、B、C的坐标利用待定系数法即可求出直线AD、BC的解析式,联立两直线解析式成方程组,通过解方程组即可求出其交点的坐标,再根据点(a,b)在如图所示的阴影部分内部(不包括边界)结合点B以及交点的横坐标即可得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,己知△ABC,任取一点O,连AO,BO,CO,并取它们的中点D,E,F,得△DEF,则下列说法正确的个数是( ) ①△ABC与△DEF是位似图形; ②△ABC与△DEF是相似图形;
③△ABC与△DEF的周长比为1:2;④△ABC与△DEF的面积比为4:1.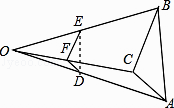
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】任何实数a,可用[a]表示不超过a的最大整数,如[4]=4,[
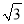 ]=1.现对72进行如下操作:72
]=1.现对72进行如下操作:72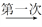 [
[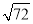 ]=8
]=8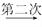 [
[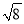 ]=2
]=2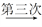 [
[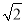 ]=1,这样对72进行3次操作后变为1,类似地,①对81进行________次操作后变为1;②进行3次操作后变为1的所有正整数中,最大的是________.
]=1,这样对72进行3次操作后变为1,类似地,①对81进行________次操作后变为1;②进行3次操作后变为1的所有正整数中,最大的是________. -
科目: 来源: 题型:
查看答案和解析>>【题目】设边长为3的正方形的对角线长为a.下列关于a的四种说法: ①a是无理数;
②a可以用数轴上的一个点来表示;
③3<a<4;
④a是18的算术平方根.
其中,所有正确说法的序号是( )
A.①④
B.②③
C.①②④
D.①③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】用“*”定义一种新运算:对于任意有理数a和b,规定a*b=ab2+2ab+a.
如:1*3=1×32+2×1×3+1=16
(1)求2*(﹣2)的值;
(2)若2*x=m,
 (其中x为有理数),试比较m,n的大小;
(其中x为有理数),试比较m,n的大小;(3)若[
 ]
] =a+4,求a的值.
=a+4,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,点E、F分别在直线AB,CD上,点P在AB、CD之间,连结EP、FP,如图1,过FP上的点G作GH∥EP,交CD于点H,且∠1=∠2.
(1)求证:AB∥CD;
(2)如图2,将射线FC沿FP折叠,交PE于点J,若JK平分∠EJF,且JK∥AB,则∠BEP与∠EPF之间有何数量关系,并证明你的结论;
(3)如图3,将射线FC沿FP折叠,将射线EA沿EP折叠,折叠后的两射线交于点M,当EM⊥FM时,求∠EPF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB=
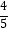 ,反比例函数y=
,反比例函数y= 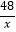 在第一象限内的图像经过点A,与BC交于点F,则△AOF的面积等于( )
在第一象限内的图像经过点A,与BC交于点F,则△AOF的面积等于( ) 
A.60
B.80
C.30
D.40
相关试题

