【题目】如图,已知反比例函数![]() 和一次函数
和一次函数![]() 的图象相交于点A和点D,且点A的横坐标为1,点D的纵坐标为-1.过点A作AB⊥x轴于点B,△AOB的面积为1.
的图象相交于点A和点D,且点A的横坐标为1,点D的纵坐标为-1.过点A作AB⊥x轴于点B,△AOB的面积为1.

(1)求反比例函数和一次函数的解析式.
(2)若一次函数![]() 的图象与x轴相交于点C,求∠ACO的度数.
的图象与x轴相交于点C,求∠ACO的度数.
(3)结合图象直接写出:当![]() 时,x的取值范围.
时,x的取值范围.
参考答案:
【答案】(1)![]() ,
, ![]() ;(2)45°;(3)
;(2)45°;(3)![]() 或
或![]() ;
;
【解析】分析:(1)由△AOB的面积为1,点A的横坐标为1,求点A的纵坐标,确定反比例函数解析式,利用反比例函数解析式求D点坐标,利用“两点法”求一次函数解析式;(2)由一次函数解析式求C点坐标,再求AB、BC,在Rt△ABC中,求tan∠ACO的值,再求∠ACO的度数;(3)当![]() 时,
时, ![]() 的图象在
的图象在![]() 的上面,由此求出x的取值范围.
的上面,由此求出x的取值范围.
本题解析:(1)∵![]() ,∴
,∴![]() OAOB=1,
OAOB=1,
又∵OB=1,∴AB=2,即A(1,2),
把A点坐标代入![]() 中,得k=2,∴y=
中,得k=2,∴y= ![]() ,
,
把y=-1代入y= ![]() 中,得x=-2,∴D(-2,-1),
中,得x=-2,∴D(-2,-1),
设直线AD解析式为y=ax+b,
将A、D两点坐标代入,得![]() ,解得
,解得 ![]() ,
,
∴y=x+1;
(2)由直线y=x+1可知,C(-1,0),则BC=OB+OC=2,AB=2,
所以,在Rt△ABC中,tan∠ACO=![]() =1,
=1,
故∠ACO=45°;
(3)由图象可知,当![]() >
>![]() 时,x<-2或0<x<1.
时,x<-2或0<x<1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设a,b是方程x2+2x﹣20=0的两个实数根,则a2+3a+b的值为( )
A.﹣18B.21C.﹣20D.18
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,菱形ABCD的顶点C的坐标为(-1,0),点B的坐标为(0,2),点A在第二象限.直线y=-
 x+5与x轴、y轴分别交于点N、M将菱形ABCD沿x轴向右平移m个单位,当点D落在△MON的内部时 (不包括三角形的边),则m的值可能是 . (写出一个即可)
x+5与x轴、y轴分别交于点N、M将菱形ABCD沿x轴向右平移m个单位,当点D落在△MON的内部时 (不包括三角形的边),则m的值可能是 . (写出一个即可)
-
科目: 来源: 题型:
查看答案和解析>>【题目】有下列命题:①无理数是无限不循环小数;②64的平方根是8;③过一点有且只有一条直线与这条直线平行;④两条直线被第三条直线所截,同位角相等,其中正确的个数是( )
A. 1B. 2C. 3D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,点P(﹣2,3)关于x轴对称的点的坐标为( )
A.(﹣2,﹣3)
B.(2,﹣3)
C.(﹣3,﹣2)
D.(3,﹣2) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=2x+4分别交x轴,y轴于点A,C,点D(m,2)在直线AC上,点B在x轴正半轴上,且OB=3OC.点E是y轴上任意一点记点E为(0,n).
(1)求直线BC的关系式;
(2)连结DE,将线段DE绕点D按顺时针旋转90°得线段DG,作正方形DEFG,是否存在n的值,使正方形DEFG的顶点F落在△ABC的边上?若存在,求出所有的n值并直接写出此时正方形DEFG与△ABC重叠部分的面积;若不存在,请说明理由.


-
科目: 来源: 题型:
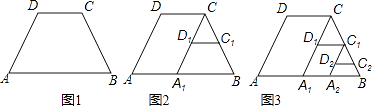
查看答案和解析>>【题目】如图1四边形ABCD中,AB∥CD,AD=DC=CB=a,∠A=60°,取AB的中点A1 , 连接A1C,再分别取A1C,BC的中点D1 , C1连接D1C1 . 得到四边形A1BC1D1 , 如图2同样方法操作得到四边形A2BC2D2 . 如图3…….如此进行下去,则四边形AnBCnDn的面积为 .
相关试题

