【题目】请认真阅读下列材料,再解决后面的问题.
依照平方根(即二次方根)和立方根(即三次方根)的定义,可给出四次方根、五次方根的定义.比如:若x2=a(a≥0),则x叫a的二次方根;若x3=a,则x叫a的三次方根:若x4=a(a≥0),则x叫a的四次方根;
(1)依照上面的材料,请你给出五次方根的定义,并求出﹣32的五次方根;
(2)解方程:![]() (2x﹣4)4﹣8=0
(2x﹣4)4﹣8=0
参考答案:
【答案】(1)如果x5=a,那么x叫做a的五次方根;-2;(2)x=3或x=1.
【解析】
(1)利用题中的阅读下列材料得出五次方根的定义,并根据五次方根的意义求解;
(2)利用四次方根的定义求解即可.
解:(1)如果x5=a,那么x叫做a的五次方根,
﹣32的五次方根为﹣2;
(2)![]() (2x﹣4)4﹣8=0,
(2x﹣4)4﹣8=0,
(2x﹣4)4﹣16=0,
(2x﹣4)4=16,
2x﹣4=±![]() ,
,
2x﹣4=±2,
x=3或x=1.
-
科目: 来源: 题型:
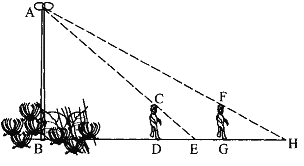
查看答案和解析>>【题目】如图,花丛中有一路灯杆AB. 在灯光下,小明在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时小明的影长GH=5米. 如果小明的身高为1.7米,求路灯杆AB的高度(精确到0.1米).
-
科目: 来源: 题型:
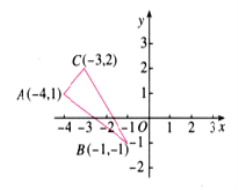
查看答案和解析>>【题目】如图,利用关于坐标轴对称的点的坐标特点
(1) 作出△ABC关于x轴对称的图象.
(2) 写出A、B、C的对应点A′、B′、C′的坐标.
(3) 直接写出△ABC的面积__________
-
科目: 来源: 题型:
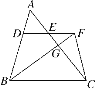
查看答案和解析>>【题目】已知如图,D是△ABC的边AB上一点,DE∥BC,交边AC于点E,延长DE至点F,使EF=DE,连接BF,交边AC于点G,连接CF.
(1)求证:
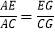 ;
;(2)如果CF2=FG·FB,求证:CG·CE=BC·DE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为a的正方形的一角剪去一个边长为b的正方形,把剩余的部分(图中的阴影部分)裁剪后拼成右边的长方形.
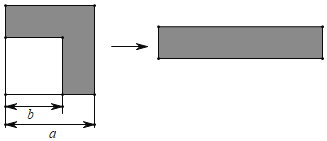
(1)请写出上述剪拼过程中所揭示的乘法公式;
(2)请运用乘法公式简便计算:20192﹣2020×2018.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图已知:E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.求证:

(1)∠ECD=∠EDC;
(2)OE是CD的垂直平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,雾霾天气给人们的生活带来很大影响,空气质量问题倍受人们关注,某学校计划在教室内安装空气净化装置,需购进A、B两种设备,已知:购买1台A种设备和2台B种设备需要3.5万元;购买2台A种设备和1台B种设备需要2.5万元.
(1)求每台A种、B种设备各多少万元?
(2)根据学校实际,需购进A种和B种设备共30台,总费用不超过30万元,请你通过计算,求至少购买A种设备多少台?
相关试题

