【题目】如图,在△ABC中,∠ACB =90°,AC = BC =2,AB =![]() ,点P是AB边上的点(异于点A,B),点Q是BC边上的点(异于点B,C),且∠CPQ =45°.当△CPQ是等腰三角形时,CQ的长为________.
,点P是AB边上的点(异于点A,B),点Q是BC边上的点(异于点B,C),且∠CPQ =45°.当△CPQ是等腰三角形时,CQ的长为________.

参考答案:
【答案】![]() 或1.
或1.
【解析】
分两种情形:①当PC=PQ时.②当PQ=CQ时分别求解即可.
解:①当PC=PQ时,∵CA=CB=2,∠ACB=90°,
∴∠A=∠B=45°,AB=![]() ,
,
∵∠CPB=∠CPQ+∠QPB=∠A+∠ACP,∠CPQ=45°,
∴∠CPQ=∠A,
∴∠ACP=∠BPQ,
∴△ACP≌△BPQ,
∴AC=PB=2,AP=BQ=![]() ,
,
∴CQ=2-(![]() )=
)=![]() ,
,
②当PQ=CQ时,∠QPC=∠QCP=45°,
∴∠ACP=∠BCP=45°,∠PQC=90°,
∴PA=PB=PC,
∵PQ⊥BC,
∴CQ=BQ=1,
故答案为:![]() 或1.
或1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点 C为线段 AB上一点,分别以 AC、BC为边在线段 AB同侧作△ACD和△BCE,且 CA=CD,CB=CE,∠ACD=∠BCE,直线 AE与 BD交于点 F
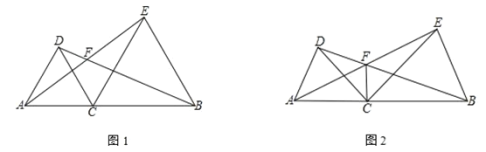
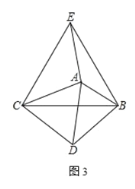
(1)如图 1,若∠ACD=60°,则∠AFD=
(2)如图 2,若∠ACD=α,连接 CF,则∠AFC= (用含α的式子表示)
(3) 将图 1 中的△ACD绕点 C顺时针旋转如图 3,连接 AE、AB、BD,∠ABD=80°,求∠EAB的度数
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图 1,△AOB中,∠AOB=90°,OA=OB,A(3,2),AB交 x轴于 C点
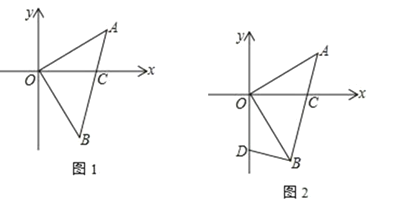
(1) 求△AOB的面积
(2) 如图2,点 D(0,
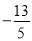 )在 y轴上,连 BD,求证:BD⊥AB
)在 y轴上,连 BD,求证:BD⊥AB -
科目: 来源: 题型:
查看答案和解析>>【题目】已知平面上
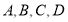 四个点.
四个点. 
(1)按下列要求画图(不写画法)
①连接
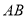 ,
,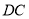 ;②作直线
;②作直线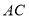 ;③作射线
;③作射线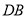 ,交
,交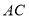 于点
于点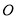 .
. (2)在(1)所画的图形中共有__________条线段,__________条射线. (所画图形中不能再添加标注其他字母);
(3)通过测量线段
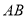 ,
,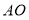 ,
,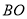 ,可知
,可知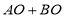 __________
__________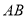 (填“
(填“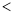 ”,“
”,“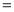 ”或“
”或“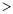 ”),可以解释这一现象的基本事实为:_______________________.
”),可以解释这一现象的基本事实为:_______________________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:抛物线
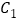 :
: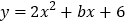 与抛物线
与抛物线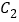 关于y轴对称, 抛物线
关于y轴对称, 抛物线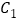 与x轴分别交于点A(-3, 0), B(m, 0), 顶点为M.
与x轴分别交于点A(-3, 0), B(m, 0), 顶点为M.(1)求b和m的值;
(2)求抛物线
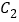 的解析式;
的解析式;(3)在x轴, y轴上分别有点P(t, 0), Q(0, -2t), 其中t>0, 当线段PQ与抛物线
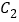 有且只有一个公共点时,求t的取值范围.
有且只有一个公共点时,求t的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.
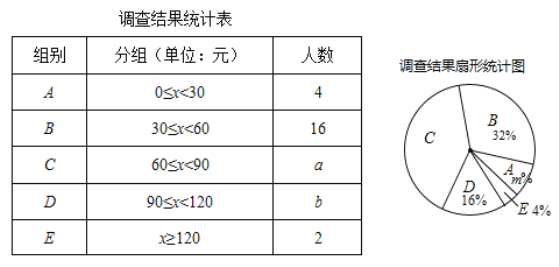
请根据以上图表,解答下列问题:
(1)填空:这次被调查的同学共有__________人,a+b=__________,m=__________;
(2)求扇形统计图中扇形C的圆心角度数;
(3)该校共有学生1000人,请估计每月零花钱的数额在60≤x<120范围的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD中,E、F分别是AB、AD边上的点,DE与CF交于点G.
(1)如图①,若四边形ABCD是矩形,且DE⊥CF,求证
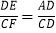 ;
;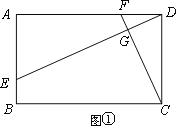


(2)如图②,若四边形ABCD是平行四边形,试探究:当∠B与∠EGC满足什么关系时,使得
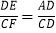 成立?并证明你的结论;
成立?并证明你的结论;(3)如图③,若BA=BC=4,DA=DC=6,∠BAD=90°,DE⊥CF,请直接写出
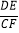 的值.
的值.
相关试题

