【题目】在平面直角坐标系中,![]() 为坐标原点,点
为坐标原点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,
,![]() 、
、![]() 、
、![]() 满足
满足![]() .
.
(1)若![]() 没有平方根,判断点
没有平方根,判断点![]() 在第几象限并说明理由;
在第几象限并说明理由;
(2)若点![]() 到
到![]() 轴的距离是点
轴的距离是点![]() 到
到![]() 轴距离的
轴距离的![]() 倍,求点
倍,求点![]() 的坐标;
的坐标;
(3)点![]() 的坐标为
的坐标为![]() ,
,![]() 的面积是
的面积是![]() 面积的
面积的![]() 倍,求点
倍,求点![]() 的坐标.
的坐标.
参考答案:
【答案】(1)![]() 点在第二象限,理由见详解;
点在第二象限,理由见详解;
(2)![]() 或
或![]() ;
;
(3)![]() 或
或![]() .
.
【解析】
(1)若![]() 没有平方根,说明
没有平方根,说明![]() ,那么
,那么![]() ,所以
,所以![]() 点在第二象限;
点在第二象限;
(2)点![]() 到
到![]() 轴的距离为
轴的距离为![]() ,点
,点![]() 到
到![]() 轴的距离为
轴的距离为![]() ,所以由题意可以列出
,所以由题意可以列出![]() ,
,
那么就有两种情况,![]() 或者
或者![]() ,将这两种情况分别代入方程组种求出
,将这两种情况分别代入方程组种求出![]() ;
;
(3)由原方程组可以得到![]() ,所以
,所以![]() 所在的线段平行于
所在的线段平行于![]() 轴,而由已知条件可以得到点
轴,而由已知条件可以得到点![]() 和点
和点![]() 在
在![]() 轴下方,则
轴下方,则![]() ,所以
,所以![]() ,解出
,解出![]() 即可解出
即可解出![]() 点的坐标;
点的坐标;
(1)![]()
![]() 没有平方根
没有平方根
![]()
![]()
![]()
![]()
![]()
![]() 点在第二象限
点在第二象限
(2)![]() 点
点![]() 到
到![]() 轴的距离是点
轴的距离是点![]() 到
到![]() 轴距离的
轴距离的![]() 倍
倍
![]()
![]()
![]()
![]() 或者
或者![]()
当![]() 时,代入原方程组可得:
时,代入原方程组可得:![]()
解得:![]()
![]()
![]()
当![]() 时,代入原方程组可得:
时,代入原方程组可得:![]()
解得:![]()
![]()
综上所述,![]() 或
或![]()
(3)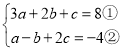
![]() 得:
得:![]()
![]()
![]()
![]() 轴
轴
![]()
![]() 的坐标为
的坐标为![]() ,
,![]() 的面积是
的面积是![]() 面积的
面积的![]() 倍
倍
![]() 点
点![]() 和点
和点![]() 在
在![]() 轴下方
轴下方
![]()
![]()
![]()
![]()
解得:![]() 或
或![]()
当![]() 时,
时,![]() ,代入原方程组可以求得
,代入原方程组可以求得![]() ;
;
当![]() 时,
时,![]() ,代入原方程组可以求得
,代入原方程组可以求得![]() ;
;
![]()
![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)(直接开平方法)2(x+3)2﹣4=0.
(2)(配方法)y2﹣6y+6=0
(3)(公式法)2x﹣1=﹣2x2 .
(4)(因式分解法)x2﹣3x﹣28=0.
(5)x(x﹣3)+x﹣3=0.
(6)x2+x﹣12=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】教育部制定《数学课程标准》要求的课程目标之一是通过数学学习,学生能够“初步学会运用数学的思维方式去观察、分析现实社会,去解决日常生活中和其他学科学习中的问题,增强应用数学的意识.”
看过2003年中央电视台春节联欢会的人们都知道,魔术节目很精彩,看后给人以思考、回味,这些看似神秘的魔术节目,很多都依据着一定的科学道理,特别是有些还与我们学习的数学知识有联系,请看下面的小魔术:
如图2所示,魔术师把4张扑克牌放在桌子上,然后蒙住眼睛,请一位观众上台,把某一张牌旋转180°.魔术师解除蒙具后,看到4张扑克牌如图3所示,他很快确定了哪一张牌被旋转过.
你知道这是怎么回事吗?试利用所学的数学知识,写一篇数学作文解释其中的道理,题目自拟,字数在200~400字之间.
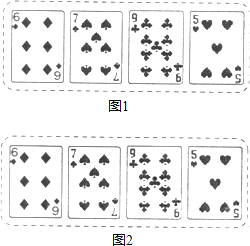
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于点F,连接CF.
(1) 求证:AD=AF;
(2) 当△ABC满足什么条件时,四边形ADCF是矩形.并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
 x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,当PC+PD最小时,点P的坐标为( )
x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,当PC+PD最小时,点P的坐标为( )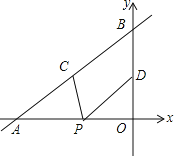
A.
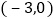 B.
B. 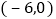 C.
C. 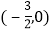 D.
D. 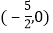
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B、C、D为矩形的四个顶点,AB=16cm,BC=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,点Q以2cm/s的速度向点D移动.当点P运动到点B停止时,点Q也随之停止运动.
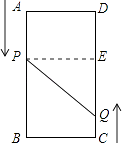
(1)问几秒后,点P和点Q的距离是10cm?
(2)问几秒后,以P、Q、D三点为顶点的三角形为直角三角形?
(提示:根据不同情况画出不同的图形,再给予解决问题.) -
科目: 来源: 题型:
查看答案和解析>>【题目】某市路桥公司决定对A、B两地之间的公路进行改造,并由甲工程队从A地向B地方向修筑,乙工程队从B地向A地方向修筑.已知甲工程队先施工2天,乙工程队再开始施工,乙工程队施工几天后因另有任务提前离开,余下的任务由甲工程队单独完成,直到公路修通.甲、乙两个工程队修公路的长度y(米)与施工时间x(天)之间的函数关系如图所示.下列说法:①乙工程队每天修公路240米;②甲工程队每天修公路120米;③甲比乙多工作6天;④A、B两地之间的公路总长是1680米.其中正确的说法有( )
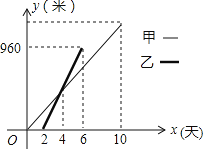
A. 4个 B. 3个 C. 2个 D. 1个
相关试题

