【题目】如图,A、B、C、D为矩形的四个顶点,AB=16cm,BC=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,点Q以2cm/s的速度向点D移动.当点P运动到点B停止时,点Q也随之停止运动.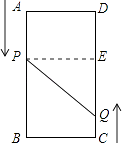
(1)问几秒后,点P和点Q的距离是10cm?
(2)问几秒后,以P、Q、D三点为顶点的三角形为直角三角形?
(提示:根据不同情况画出不同的图形,再给予解决问题.)
参考答案:
【答案】
(1)解:设x秒后,点P和点Q的距离是10cm,
(16﹣2x﹣3x)2+62=102,
(16﹣5x)2=64,
16﹣5x=±8,
x1=1.6,x2=4.8,
答:1.6秒或4.8秒时,点P和点Q的距离是10cm;
(2)解:∵四边形ABCD是矩形,
∴CD=AB=16,AD=BC=6,
根据题意得:AP=3t,CQ=2t,
∴DQ=CD﹣CQ=16﹣2t,
过点Q作QM⊥AB于点M,
∴四边形BCQM是矩形,
∴QM=BC=6,BM=CQ=2t,
∴PM=AB﹣AP﹣BM=16﹣5t,
①如图1, 
若∠DPQ=90°,
∴∠APD+∠MPQ=90°,
∵∠APD=∠ADP=90°,
∴∠ADP=∠MPQ,
∵∠A=∠PMQ=90°,
∴△APD∽△MQP,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得:t=2或t= ![]() ;
;
②如图2, 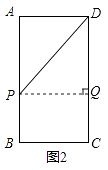
若∠DQP=90°,则有DQ2=DP2﹣PQ2,
∴(16﹣2t)2=62+(3t)2﹣62,
解得:t= ![]() ,
,
综上所述,当t=2或 ![]() 或
或 ![]() 时,△PDQ为直角三角形.
时,△PDQ为直角三角形.
【解析】(1)根据矩形的性质和勾股定理,得到一元二次方程,求出这个一元二次方程的解即可;(2)根据矩形的性质和速度得到各个边的关系式,当∠DPQ=90°时,得到△APD∽△MQP,得到比例求出t的值;当∠DQP=90°时,根据勾股定理求出t的值,在解一元二次方程时,注意实际意义.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于点F,连接CF.
(1) 求证:AD=AF;
(2) 当△ABC满足什么条件时,四边形ADCF是矩形.并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,
 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为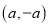 ,点
,点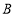 坐标为
坐标为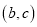 ,
,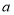 、
、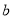 、
、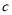 满足
满足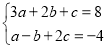 .
.(1)若
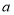 没有平方根,判断点
没有平方根,判断点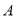 在第几象限并说明理由;
在第几象限并说明理由;(2)若点
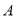 到
到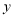 轴的距离是点
轴的距离是点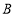 到
到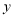 轴距离的
轴距离的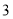 倍,求点
倍,求点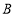 的坐标;
的坐标;(3)点
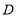 的坐标为
的坐标为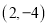 ,
,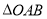 的面积是
的面积是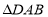 面积的
面积的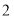 倍,求点
倍,求点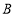 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
 x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,当PC+PD最小时,点P的坐标为( )
x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,当PC+PD最小时,点P的坐标为( )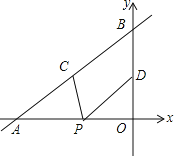
A.
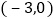 B.
B. 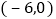 C.
C. 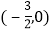 D.
D. 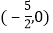
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市路桥公司决定对A、B两地之间的公路进行改造,并由甲工程队从A地向B地方向修筑,乙工程队从B地向A地方向修筑.已知甲工程队先施工2天,乙工程队再开始施工,乙工程队施工几天后因另有任务提前离开,余下的任务由甲工程队单独完成,直到公路修通.甲、乙两个工程队修公路的长度y(米)与施工时间x(天)之间的函数关系如图所示.下列说法:①乙工程队每天修公路240米;②甲工程队每天修公路120米;③甲比乙多工作6天;④A、B两地之间的公路总长是1680米.其中正确的说法有( )
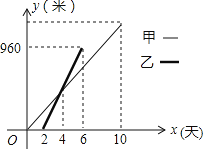
A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
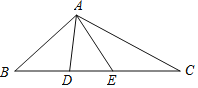
查看答案和解析>>【题目】如图,△ABC的两边AB和AC的垂直平分线分别交BC于D,E,若∠BAC+∠DAE=150°,则∠BAC的度数是( )
A.
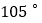 B.
B. 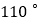 C.
C. 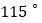 D.
D. 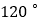
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=80°,OM是∠AOB的平分线,∠BOC=20°,ON是∠BOC的平分线,则∠MON的度数为( )
A.30° B.40° C.50° D.30°或50°
相关试题

