【题目】教育部制定《数学课程标准》要求的课程目标之一是通过数学学习,学生能够“初步学会运用数学的思维方式去观察、分析现实社会,去解决日常生活中和其他学科学习中的问题,增强应用数学的意识.”
看过2003年中央电视台春节联欢会的人们都知道,魔术节目很精彩,看后给人以思考、回味,这些看似神秘的魔术节目,很多都依据着一定的科学道理,特别是有些还与我们学习的数学知识有联系,请看下面的小魔术:
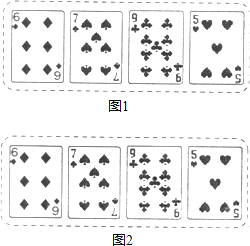
如图2所示,魔术师把4张扑克牌放在桌子上,然后蒙住眼睛,请一位观众上台,把某一张牌旋转180°.魔术师解除蒙具后,看到4张扑克牌如图3所示,他很快确定了哪一张牌被旋转过.
你知道这是怎么回事吗?试利用所学的数学知识,写一篇数学作文解释其中的道理,题目自拟,字数在200~400字之间.
参考答案:
【答案】见解析
【解析】
认真观察和思考发现,由于图1中的四张牌与图2中的牌完全相同.似乎没有牌被动过,所以旋转后的图形与原图形完全一样,那么被动过的这张牌上的图案一定是中心对称图形.
解:第一张扑克牌即方块6被观众旋转过.
认牌魔术
魔术原本是一种西洋艺术,既美观又神秘,主要锻炼手和脑的灵活度.以前,我很喜欢刘谦表演的魔术,因为我觉得他表演的魔术特别有趣、神奇.虽然知道是假的,但有时候还会自己试试,可是根本就没变出什么来.
学习了中心对称图形和旋转的性质后,我发现这四张扑克牌中后三张上的图案,都不是中心对称图形.若它们被旋转过,则与原来的图案是不同的,魔术师通过观察发现后三张扑克牌没有变化,那么变化的自然是第一张扑克牌了.由于方块6的图案是中心对称图形,旋转过的图案与原图案完全一样,故选方块6.原来这蕴含了我们学习中的知识点的.
这真是一个有趣的魔术,它也是我亲自动手完成一个小魔术.它让我明白了在生活和学习中要善于观察和发现.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人共同计算一道整式乘法:(2x+a)(3x+b),由于甲抄错了第一个多项式中a的符号,得到的结果为6x2+11x-10;由于乙漏抄了第二个多项式中的x的系数,得到的结果为2x2-9x+10.请你计算出a,b的值各是多少,并写出这道整式乘法的正确结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小龙在学校组织的社会调查活动中负责了解他所居住的小区450户居民的家庭收入情况、他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.

分组
频数
百分比
600≤x<800
2
5%
800≤x<1000
6
15%
1000≤x<1200
45%
9
22.5%
1600≤x<1800
2
合计
40
100%
根据以上提供的信息,解答下列问题:
(1)补全频数分布表;
(2)补全频数分布直方图;
(3)请你估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有多少户? -
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)(直接开平方法)2(x+3)2﹣4=0.
(2)(配方法)y2﹣6y+6=0
(3)(公式法)2x﹣1=﹣2x2 .
(4)(因式分解法)x2﹣3x﹣28=0.
(5)x(x﹣3)+x﹣3=0.
(6)x2+x﹣12=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于点F,连接CF.
(1) 求证:AD=AF;
(2) 当△ABC满足什么条件时,四边形ADCF是矩形.并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,
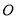 为坐标原点,点
为坐标原点,点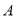 的坐标为
的坐标为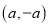 ,点
,点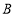 坐标为
坐标为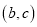 ,
,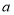 、
、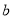 、
、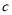 满足
满足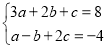 .
.(1)若
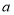 没有平方根,判断点
没有平方根,判断点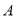 在第几象限并说明理由;
在第几象限并说明理由;(2)若点
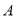 到
到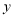 轴的距离是点
轴的距离是点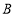 到
到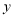 轴距离的
轴距离的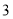 倍,求点
倍,求点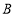 的坐标;
的坐标;(3)点
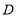 的坐标为
的坐标为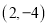 ,
,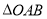 的面积是
的面积是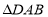 面积的
面积的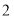 倍,求点
倍,求点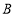 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
 x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,当PC+PD最小时,点P的坐标为( )
x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,当PC+PD最小时,点P的坐标为( )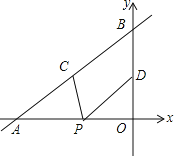
A.
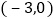 B.
B. 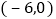 C.
C. 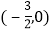 D.
D. 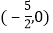
相关试题

