搜索
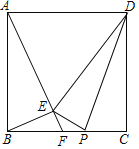
【题目】如图，已知四边形ABCD是边长为3的正方形，动点P从点B出发，沿BC向终点C运动，点P可以与点B、点C重合，连接PD，将
沿直线PD折叠，设折叠后点C的对应点为点E，连接AE并延长交BC于点F，连接BE，则下列结论中：
当
时，
为等边三角形；
当时，F为BC的中点；
当
时，
；
当点P从点B运动到点C时，点E所走过的路径的长为
其中正确的有
A. 1个 B. 2个 C. 3个 D. 4个
参考答案：
【答案】C
【解析】
根据题意可得
为等边三角形，因此可判断
，由E点所走过的路径是以D为圆心，CD为半径的
圆可判断
由沿直线PD折叠得到
可得CE的长，根据相似可得EM，BM的长，以B点为原点，BC为x轴，AB为y轴建立直角坐标系，可求AE，BE解析式，根据
，两直线垂直，可判断
．
解：
且将
沿直线PD折叠得到
，
，
即
且
为等边三角形
，
且
故
正确，
错误
是定值3，
点E所走过的路径是以D为圆心，DC长为半径的圆
点E所走过的路径
故
正确
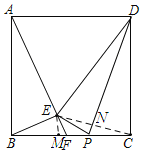
连接EC交DP于N，作
，
由勾股定理得：
将沿直线PD折叠得到
，
，
，
∽
，
以B点为原点，BC为x轴，AB为y轴建立直角坐标系
，
可得BE解析式
，
AE解析式
故正确
故选：C．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，
是等边三角形，
是直线
上一点，以为顶点做
． 
交过
且平行于
的直线于
，求证：
；当为的中点时，（如图1）小明同学很快就证明了结论：他的做法是：取的中点
，连结
，然后证明
． 从而得到，我们继续来研究：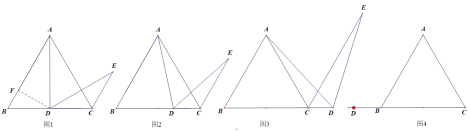
（1）如图2、当D是BC上的任意一点时，求证：
（2）如图3、当D在BC的延长线上时，求证：
（3）当
在
的延长线上时，请利用图4画出图形，并说明上面的结论是否成立（不必证明）． -
科目： 来源： 题型：
查看答案和解析>>【题目】（1）如图1，∠MAN=90°，射线AE在这个角的内部，点B、C分别在∠MAN的边AM、AN上，且AB=AC，CF⊥AE于点F，BD⊥AE于点D．求证：△ABD≌△CAF；
（2）如图2，点B、C分别在∠MAN的边AM、AN上，点E、F都在∠MAN内部的射线AD上，∠1、∠2分别是△ABE、△CAF的外角．已知AB=AC，且∠1=∠2=∠BAC．求证：△ABE≌△CAF；
（3）如图3，在△ABC中，AB=AC，AB＞BC．点D在边BC上，CD=2BD，点E、F在线段AD上，∠1=∠2=∠BAC．若△ABC的面积为15，求△ACF与△BDE的面积之和．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，CE、CB分别是△ABC与△ADC的中线，且∠ACB=∠ABC．求证：CD=2CE．
-
科目： 来源： 题型：
查看答案和解析>>【题目】龙华区某学校开展“四点半课堂”，计划开设以下课外活动项目：
版画、
机器人、
航模、
园艺种植
为了解学生最喜欢哪一种活动项目，随机抽取了部分学生进行调查
每位学生必须选且只能选其中一个项目
，并将调查结果绘制成了如图1、2的两幅不完整的统计图，请根据图中的信息回答下列问题：
这次被调查的学生共有______人；图1中，选“版画“所在扇形的圆心角度数为______
；
请将图2的条形统计图补充完整；
若该校学生总人数为1500人，由于”机器人“项目因故取消，原选“机器人”中
的学生转选了“航模”项目，则该校学生中选“航模“项目的总人数为______人 -
科目： 来源： 题型：
查看答案和解析>>【题目】一蓄水池有水40m3，按一定的速度放水，水池里的水量y（m3）与放水时间t（分）有如下关系：
放水时间（分）
1
2
3
4
…
水池中水量（m3）
38
36
34
32
…
下列结论中正确的是（ ）
A. y随t的增加而增大
B. 放水时间为15分钟时，水池中水量为8m3
C. 每分钟的放水量是2m3
D. y与t之间的关系式为y＝40t
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图．在△ABC，△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，点C，D，E三点在同一条直线上，连接BD，BE．以下四个结论：
①BD=CE；②∠ACE+∠DBC=45°；③BD⊥CE；④∠BAE+∠DAC=180°．
其中正确的有______．
相关试题
