【题目】如图:△ABC中,![]() ACB=90°,AC=BC,AB=4,点E在BC上,且BE=2,点P在
ACB=90°,AC=BC,AB=4,点E在BC上,且BE=2,点P在![]() ABC的平分线BD上运动,则PE+PC的长度最小值为()
ABC的平分线BD上运动,则PE+PC的长度最小值为()
A.1
B.![]()
C.![]()
D.![]()
参考答案:
【答案】B
【解析】作点E关于BD的对称点E',连接E'C,如下图: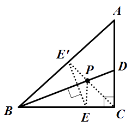
∵BD是∠ ABC的平分线,
∴通过作图知,BP垂直平分EE',
∴PE'=PE
∴此时PE+PC=PE'+PC=E'C,PE+PC的长度最小,
∵点E、点E'关于BD的对称,∴BE'=BE=2,
又∵AB=4,∴点E'是AB中点,CE'是中线.
∵△ABC中, ∠ ACB=90°,AC=BC,
∴△ABC是等腰直角三角形,∠ ABC=45![]() ,
,
∴CE'又是底边AB的高,
∴△BE'C也是等腰直角三角形,
∴E'C=2,
即:PE+PC的长度最小值为2.
故选B.
【考点精析】根据题目的已知条件,利用三角形的“三线”和轴对称-最短路线问题的相关知识可以得到问题的答案,需要掌握1、三角形角平分线的三条角平分线交于一点(交点在三角形内部,是三角形内切圆的圆心,称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部,是三角形的几何中心,称为中心);3、三角形的高线是顶点到对边的距离;注意:三角形的中线和角平分线都在三角形内;已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程组:

-
科目: 来源: 题型:
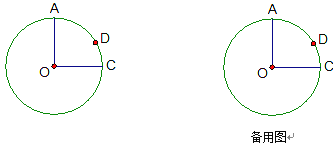
查看答案和解析>>【题目】如图,⊙O的半径OA⊥OC,点D在
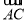 上,且
上,且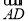 =2
=2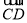 ,OA=4.
,OA=4.(1)∠COD= °;
(2)求弦AD的长;
(3)P是半径OC上一动点,连结AP、PD,请求出AP+PD的最小值,并说明理由.
(解答上面各题时,请按题意,自行补足图形)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 面积为8,AD为BC边上的中线,
面积为8,AD为BC边上的中线,  为
为  上任意一点,连接
上任意一点,连接  ,
,  ,图中阴影部分的面积为( )
,图中阴影部分的面积为( )
A.
B.
C.4
D.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣32×(﹣5)+16÷(﹣2)3﹣|﹣4×5|
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国实施的“一带一路”战略方针,惠及沿途各国.中欧班列也已融入其中.从我国重庆开往德国的杜伊斯堡班列,全程约11025千米.同样的货物,若用轮船运输,水路路程是铁路路程的1.6倍,水路所用天数是铁路所用天数的3倍,列车平均日速(平均每日行驶的千米数)是轮船平均日速的2倍少49千米.分别求出列车及轮船的平均日速.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=10x-6一定不经过第_____象限(“一”、“二”、“三”或“四”)。
相关试题

