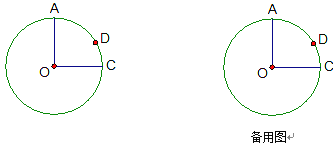
【题目】如图,⊙O的半径OA⊥OC,点D在![]() 上,且
上,且![]() =2
=2![]() ,OA=4.
,OA=4.
(1)∠COD= °;
(2)求弦AD的长;
(3)P是半径OC上一动点,连结AP、PD,请求出AP+PD的最小值,并说明理由.
(解答上面各题时,请按题意,自行补足图形)
参考答案:
【答案】(1)30;(2)弦AD长为4;(3)AP+PD的最小值为![]() ,理由见解析.
,理由见解析.
【解析】(本小题满分12分)
解:(1)30;……………………………………………………………………1分
(2)连结OD、AD(如图2).
∵OA⊥OC,∴∠AOC=90°.∵![]() =2
=2![]() ,
,
设![]() 所对的圆心角∠COD=
所对的圆心角∠COD=![]() ,………………………………………………1分
,………………………………………………1分
则∠AOD=![]() ,…………………………………………………………………2分
,…………………………………………………………………2分
由∠AOD+∠DOC=90°,
得![]() +
+![]() =90°,∴
=90°,∴![]() =30°,
=30°,![]() =60°,…………………………3分
=60°,…………………………3分
即∠AOD=60°,又∵OA=OD,∴△AOD为等边三角形,…………4分
∴AD=OA=4;…………………………………………………………………5分
(3)过点D作DE⊥OC,交⊙O于点E,……………………………………1分
连结AE,交OC于点P(如图3),………………………………………………2分
则此时,AP+PD的值最小.
∵根据圆的对称性,点E是点D关于OC的对称点,
OC是DE的垂直平分线,即PD=PE.………………………………………3分
∴AP+PD=AP+PE=AE,
若在OC上另取一点F,连结AF、FD及EF,
在△AFE中,AF+FE>AE,
即AF+FE>AP+PD,
∴可知AP+PD最小.…………………………………………………………4分
∵∠AED=![]() ∠AOD=30°,
∠AOD=30°,
又∵OA⊥OC,DE⊥OC,∴OA∥DE,
∴∠OAE=∠AED=30°.
延长AO交⊙O于点B,连结BE,∵AB为直径,
∴△ABE为直角三角形.由![]() =cos∠BAE,……………………………5分
=cos∠BAE,……………………………5分
得AE=AB·cos30°=2×4×![]() =
=![]() ,……………………………6分
,……………………………6分
即AP+PD=![]() ,
,
[也可利用勾股定理求得AE]
-
科目: 来源: 题型:
查看答案和解析>>【题目】天宫二号在太空绕地球一周大约飞行42500千米,将42500用科学记数法表示为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在创建全国森林城市的活动中,我区一“青年突击队”决定义务整修一条1000米长的绿化带,开工后,附近居民主动参加到义务劳动中,使整修的速度比原计划提高了一倍,结果提前4小时完成任务,问“青年突击队”原计划每小时整修多少米长的绿化带?
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程组:

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 面积为8,AD为BC边上的中线,
面积为8,AD为BC边上的中线,  为
为  上任意一点,连接
上任意一点,连接  ,
,  ,图中阴影部分的面积为( )
,图中阴影部分的面积为( )
A.
B.
C.4
D.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:△ABC中,
 ACB=90°,AC=BC,AB=4,点E在BC上,且BE=2,点P在
ACB=90°,AC=BC,AB=4,点E在BC上,且BE=2,点P在 ABC的平分线BD上运动,则PE+PC的长度最小值为()
ABC的平分线BD上运动,则PE+PC的长度最小值为()
A.1
B.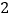
C.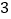
D.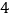
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣32×(﹣5)+16÷(﹣2)3﹣|﹣4×5|
相关试题

