【题目】如图,在平面直角坐标系xOy中,直线![]() 的表达式为
的表达式为![]() ,点A,B的坐标分别为
,点A,B的坐标分别为
(1,0),(0,2),直线AB与直线![]() 相交于点P.
相交于点P.
(1)求直线AB的表达式;
(2)求点P的坐标;
(3)若直线![]() 上存在一点C,使得△APC的面积是△APO的面积的2倍,直接写出点C的坐标.
上存在一点C,使得△APC的面积是△APO的面积的2倍,直接写出点C的坐标.

参考答案:
【答案】(1) y=-2x+2 ;(2) P的坐标为(2,-2);(3) (3,0),(1,-4).
【解析】(1)用待定系数法求函数的解析式;(2)由两个解析式构成方程组,解方程组可得交点的坐标;(3)点P可能在P的上方或下方,结合图形进行分析计算.
解:(1)设直线AB的表达式为y=kx+b.
由点A,B的坐标分别为(1,0),(0,2),
可知![]()
解得![]()
所以直线AB的表达式为y=-2x+2.
(2)由题意,
得![]()
解得![]()
所以点P的坐标为(2,-2).
(3)(3,0),(1,-4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】为迎接“国家卫生城市”复检,某市环卫局准备购买A、B两种型号的垃圾箱,通过市场调研得知:购买3个A型垃圾箱和2个B型垃圾箱共需540元;购买2个A型垃圾箱比购买3个B型垃圾箱少用160元.
(1)每个A型垃圾箱和B型垃圾箱各多少元?
(2)现需要购买A,B两种型号的垃圾箱共300个,分别由甲、乙两人进行安装,要求在12天内完成(两人同时进行安装).已知甲负责A型垃圾箱的安装,每天可以安装15个,乙负责B型垃圾箱的安装,每天可以安装20个,生产厂家表示若购买A型垃圾箱不少于150个时,该型号的产品可以打九折;若购买B型垃圾箱超过150个时,该型号的产品可以打八折,若既能在规定时间内完成任务,费用又最低,应购买A型和B型垃圾箱各多少个?最低费用是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
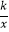 的图象经过点A(﹣1,4),直线y=﹣x+b(b≠0)与双曲线y=
的图象经过点A(﹣1,4),直线y=﹣x+b(b≠0)与双曲线y= 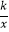 在第二、四象限分别相交于P,Q两点,与x轴、y轴分别相交于C,D两点.
在第二、四象限分别相交于P,Q两点,与x轴、y轴分别相交于C,D两点. 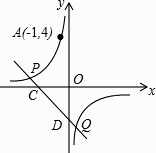
(1)求k的值;
(2)当b=﹣2时,求△OCD的面积;
(3)连接OQ,是否存在实数b,使得S△ODQ=S△OCD?若存在,请求出b的值;若不存在,请说明理由.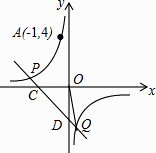
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
小明想探究函数
 的性质,他借助计算器求出了y与x的几组对应值,并在平面直角坐标系中画出了函数图象:
的性质,他借助计算器求出了y与x的几组对应值,并在平面直角坐标系中画出了函数图象:x
…
-3
-2
-1
1
2
3
…
y
…
2.83
1.73
0
0
1.73
2.83
…

小聪看了一眼就说:“你画的图象肯定是错误的.”
请回答:小聪判断的理由是_____________.请写出函数
 的一条性质:_____________.
的一条性质:_____________. -
科目: 来源: 题型:
查看答案和解析>>【题目】将正方体骰子(相对面上的点数分别为1和6、2和5、3和4)放置于水平桌面上,如图1。在图2中,将骰子向右翻滚90°,然后在桌面上按逆时针方向旋转90°,则完成一次变换。若骰子的初始位置为图1所示的状态,那么按上述规则连续完成14次变换后,骰子朝上一面的点数是_____________________。

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校七年级(1)班班主任对本班学生进行了“我最喜欢的课外活动”的调查,并将调查结果分为书法和绘画类(记为A)、音乐类(记为B)、球类(记为C)、其它类(记为D).根据调查结果发现该班每个学生都进行了登记且每人只登记了一种自己最喜欢的课外活动.班主任根据调查情况把学生进行了归类,并制作了如下两幅统计图.请你结合图中所给信息解答下列问题:
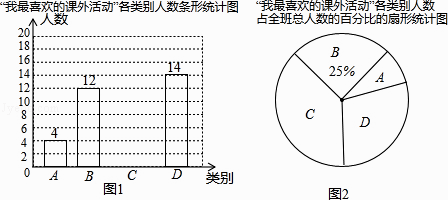
(1)七年级(1)班学生总人数为人,扇形统计图中D类所对应扇形的圆心角为度,请补全条形统计图;
(2)学校将举行书法和绘画比赛,每班需派两名学生参加,A类4名学生中有两名学生擅长书法,另两名学生擅长绘画.班主任现从A类4名学生中随机抽取两名学生参加比赛,请你用列表或画树状图的方法求出抽到的两名学生恰好是一名擅长书法,另一名擅长绘画的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:2sin45°﹣3﹣2+
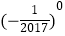 +|
+| 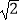 ﹣2|+
﹣2|+ 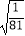 .
.
相关试题

