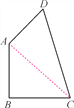
【题目】如图,在四边形ABCD中,AB=BC=1,CD=![]() ,DA=1,且∠B=90°.求:
,DA=1,且∠B=90°.求:
(1)∠BAD的度数;
(2)四边形ABCD的面积(结果保留根号).
参考答案:
【答案】(1)135°;(2)![]()
【解析】试题分析:(1)由于AB=BC=1,且∠B=90°根据勾股定理即可求出AC的长度,而CD=![]() ,DA=1,利用勾股定理的逆定理即可证明△ACD是直角三角形,由此即可求出∠BAD的度数;
,DA=1,利用勾股定理的逆定理即可证明△ACD是直角三角形,由此即可求出∠BAD的度数;
(2)首先把求四边形ABCD的面积分割为求△ABC和△ACD的面积,然后利用三角形的面积公式可以分别求出这两个三角形的面积,最后就可以求出四边形ABCD的面积.
试题解析:(1)∵AB=BC=1,且∠B=90°,
∴∠BAC=45°,AC=![]() ,
,
而CD=![]() ,DA=1,
,DA=1,
∴CD2=AD2+AC2,
∴△ACD是直角三角形,即∠DAC=90°,
∴∠BAD=∠BAC+∠DAC=135°;
(2)∵S四边形ABCD=S△ABC+S△ACD,
而S△ABC=![]() AB×BC=
AB×BC=![]() ,
,
S△ACD=![]() AD×CD=
AD×CD=![]() ,
,
∴S四边形ABCD=S△ABC+S△ACD=![]()
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学决定在学生中开展丢沙包、打篮球、跳大绳和踢毽球四种项目的活动,为了解学生对四种项目的喜欢情况,随机调查了该校m名学生最喜欢的一种项目(每名学生必选且只能选择四种活动项目的一种),并将调查结果绘制成如下的不完整的统计图表:
学生最喜欢的活动项目的人数统计表
项目
学生数(名)
百分比
丢沙包
20
10%
打篮球
60
p%
跳大绳
n
40%
踢毽球
40
20%
根据图表中提供的信息,解答下列问题:
(1)m= ,n= ,p= ;
(2)请根据以上信息直接补全条形统计图;

(3)根据抽样调查结果,请你估计该校2000名学生中有多少名学生最喜欢跳大绳.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD、AC分别交于点E、F,且∠ACB=∠DCE.
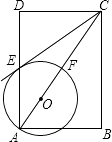
(1)判断直线CE与⊙O的位置关系,并证明你的结论;
(2)若tan∠ACB=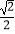 ,BC=2,求⊙O的半径.
,BC=2,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了美化校园环境,争创绿色学校,某县教育局委托园林公司对A,B两校进行校园绿化,已知A校有如图
 的阴影部分空地需铺设草坪,B校有如图
的阴影部分空地需铺设草坪,B校有如图 的阴影部分空地需铺设草坪,在甲、乙两地分别有同种草皮3500米
的阴影部分空地需铺设草坪,在甲、乙两地分别有同种草皮3500米 和2500米
和2500米 出售,且售价一样,若园林公司向甲、乙两地购买草皮,其路程和运费单价表如下:
出售,且售价一样,若园林公司向甲、乙两地购买草皮,其路程和运费单价表如下:路程、运费单价表
A校
B校
路程
 千米
千米
运费单价
 元
元
路程
 千米
千米
运费单价
 元
元
甲地
20

10

乙地
15

20
 注:运费单价表示每平方米草皮运送1千米所需的人民币
注:运费单价表示每平方米草皮运送1千米所需的人民币

求:
 分别求出图1、图2的阴影部分面积;
分别求出图1、图2的阴影部分面积; 若园林公司将甲地
若园林公司将甲地 的草皮全部运往A校,请你求出园林公司运送草皮去A、B两校的总运费;
的草皮全部运往A校,请你求出园林公司运送草皮去A、B两校的总运费; 请你给出一种运送方案,使得园林公司支付出送草皮的总运费不超过15000元.
请你给出一种运送方案,使得园林公司支付出送草皮的总运费不超过15000元. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,三边分别为下列长度,判断该三角形是不是直角三角形,并指出哪一个角是直角.
(1)a=
 ,b=2
,b=2 ,c=
,c= ;
;(2)a=5,b=7,c=9;
(3)a=2,b=
 ,c=
,c= ;
;(4)a=5,b=2
 ,c=1.
,c=1. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,将一副直角三角板放在同一条直线AB上,其中
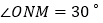 ,
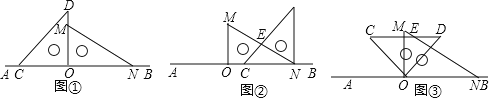
,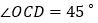 .
.
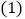 将图1中的三角尺OCD沿AB的方向平移至图
将图1中的三角尺OCD沿AB的方向平移至图 的位置,使得点O与点N重合,CD与MN相交于点E,求
的位置,使得点O与点N重合,CD与MN相交于点E,求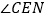 的度数;
的度数;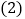 将图1中的三角尺OCD绕点O按顺时针方向旋转,使一边OD在
将图1中的三角尺OCD绕点O按顺时针方向旋转,使一边OD在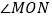 的内部,如图3,且OD恰好平分
的内部,如图3,且OD恰好平分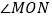 ,CD与MN相交于点E,求
,CD与MN相交于点E,求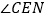 的度数;
的度数; 将图1中的三角尺OCD绕点O按每秒
将图1中的三角尺OCD绕点O按每秒 的速度沿顺时针方向旋转一周,在旋转的过程中,在第______ 秒时,边CD恰好与边MN平行;在第______ 秒时,直线CD恰好与直线MN垂直
的速度沿顺时针方向旋转一周,在旋转的过程中,在第______ 秒时,边CD恰好与边MN平行;在第______ 秒时,直线CD恰好与直线MN垂直 直接写出结果
直接写出结果
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的5个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:

(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)如果要在这5个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
相关试题

