【题目】为了美化校园环境,争创绿色学校,某县教育局委托园林公司对A,B两校进行校园绿化,已知A校有如图![]() 的阴影部分空地需铺设草坪,B校有如图
的阴影部分空地需铺设草坪,B校有如图![]() 的阴影部分空地需铺设草坪,在甲、乙两地分别有同种草皮3500米
的阴影部分空地需铺设草坪,在甲、乙两地分别有同种草皮3500米![]() 和2500米
和2500米![]() 出售,且售价一样,若园林公司向甲、乙两地购买草皮,其路程和运费单价表如下:
出售,且售价一样,若园林公司向甲、乙两地购买草皮,其路程和运费单价表如下:
路程、运费单价表
A校 | B校 | |||
路程 | 运费单价 | 路程 | 运费单价 | |
甲地 | 20 |
| 10 |
|
乙地 | 15 |
| 20 | |
![]() 注:运费单价表示每平方米草皮运送1千米所需的人民币
注:运费单价表示每平方米草皮运送1千米所需的人民币![]()

求:![]() 分别求出图1、图2的阴影部分面积;
分别求出图1、图2的阴影部分面积;
![]() 若园林公司将甲地
若园林公司将甲地![]() 的草皮全部运往A校,请你求出园林公司运送草皮去A、B两校的总运费;
的草皮全部运往A校,请你求出园林公司运送草皮去A、B两校的总运费;
![]() 请你给出一种运送方案,使得园林公司支付出送草皮的总运费不超过15000元.
请你给出一种运送方案,使得园林公司支付出送草皮的总运费不超过15000元.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)20400元;(3)见解析.
;(2)20400元;(3)见解析.
【解析】(1)平移图形后,利用平行四边形面积公式计算即可.
(2)总费用=园林公司将甲地3500m2的草皮全部运往A校的费用+园林公司将乙地100m2的草皮全部运往A校的费用+园林公司将乙地2400m2的草皮全部运往B校的费用.
(3)设甲地草皮运送x m2去A校,有(3500﹣x)m2运往B校,乙地草皮(3600﹣x)m2运往A校,(x﹣1100)m2草皮运往B校.根据题意列出不等式即可解决问题.
(1)图1阴影面积=90×40=3600m2,图2阴影面积=40×60=2400m2.
(2)总运费=3500×20×0.15+100×15×0.2+2400×20×0.2=20400元.
(3)设甲地草皮运送x m2去A校,有(3500﹣x)m2运往B校,乙地草皮(3600﹣x)m2运往A校,(x﹣1100)m2草皮运往B校.依题意得:
20×0.15x+(3500﹣x)×10×0.15+(3600﹣x)×15×0.20+(x﹣1100)×20×0.20≤1500,且x﹣1100≥0,
解得:1100≤x≤1340.
只要所设计的方案中运往A校的草皮在1100m2~1340m2之间都可.如甲地的草皮运往A校1100m2,运往B校2400m2,乙地草皮运往A校2500m2,总运费14400元.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两同学同时从山脚开始爬山,到达山顶后立即下山,在山脚和山顶之间不断往返运动,已知山坡长为360m,甲、乙上山的速度比是6:4,并且甲、乙下山的速度都是各自上山速度的1.5倍,当甲第三次到达山顶时,则此时乙所在的位置是
 。
。 -
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学决定在学生中开展丢沙包、打篮球、跳大绳和踢毽球四种项目的活动,为了解学生对四种项目的喜欢情况,随机调查了该校m名学生最喜欢的一种项目(每名学生必选且只能选择四种活动项目的一种),并将调查结果绘制成如下的不完整的统计图表:
学生最喜欢的活动项目的人数统计表
项目
学生数(名)
百分比
丢沙包
20
10%
打篮球
60
p%
跳大绳
n
40%
踢毽球
40
20%
根据图表中提供的信息,解答下列问题:
(1)m= ,n= ,p= ;
(2)请根据以上信息直接补全条形统计图;

(3)根据抽样调查结果,请你估计该校2000名学生中有多少名学生最喜欢跳大绳.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD、AC分别交于点E、F,且∠ACB=∠DCE.
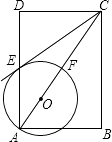
(1)判断直线CE与⊙O的位置关系,并证明你的结论;
(2)若tan∠ACB=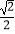 ,BC=2,求⊙O的半径.
,BC=2,求⊙O的半径. -
科目: 来源: 题型:
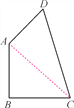
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=BC=1,CD=
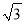 ,DA=1,且∠B=90°.求:
,DA=1,且∠B=90°.求:(1)∠BAD的度数;
(2)四边形ABCD的面积(结果保留根号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,三边分别为下列长度,判断该三角形是不是直角三角形,并指出哪一个角是直角.
(1)a=
 ,b=2
,b=2 ,c=
,c= ;
;(2)a=5,b=7,c=9;
(3)a=2,b=
 ,c=
,c= ;
;(4)a=5,b=2
 ,c=1.
,c=1. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,将一副直角三角板放在同一条直线AB上,其中
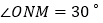 ,
,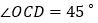 .
.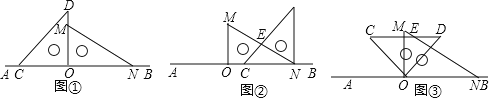
 将图1中的三角尺OCD沿AB的方向平移至图
将图1中的三角尺OCD沿AB的方向平移至图 的位置,使得点O与点N重合,CD与MN相交于点E,求
的位置,使得点O与点N重合,CD与MN相交于点E,求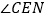 的度数;
的度数;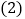 将图1中的三角尺OCD绕点O按顺时针方向旋转,使一边OD在
将图1中的三角尺OCD绕点O按顺时针方向旋转,使一边OD在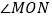 的内部,如图3,且OD恰好平分
的内部,如图3,且OD恰好平分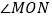 ,CD与MN相交于点E,求
,CD与MN相交于点E,求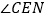 的度数;
的度数; 将图1中的三角尺OCD绕点O按每秒
将图1中的三角尺OCD绕点O按每秒 的速度沿顺时针方向旋转一周,在旋转的过程中,在第______ 秒时,边CD恰好与边MN平行;在第______ 秒时,直线CD恰好与直线MN垂直
的速度沿顺时针方向旋转一周,在旋转的过程中,在第______ 秒时,边CD恰好与边MN平行;在第______ 秒时,直线CD恰好与直线MN垂直 直接写出结果
直接写出结果
相关试题

