【题目】已知一次函数y=![]() x-15的图象与x轴,y轴分别交于点A,B,O为坐标原点,则在△OAB内部(包括边界),纵坐标、横坐标都是整数的点(整点)共有_________个.
x-15的图象与x轴,y轴分别交于点A,B,O为坐标原点,则在△OAB内部(包括边界),纵坐标、横坐标都是整数的点(整点)共有_________个.
参考答案:
【答案】106
【解析】分析: 求出A、B的坐标,分别求出横坐标是1、2、3、4、5、6、7、8、9、10、11的纵坐标,即可得出横坐标是1、2、3、4…时点的个数,再加上在两坐标轴上的点,即可得到答案.
详解: 当x=0时,y=-15,∴B(0,-15),
当y=0时,0=![]() x-15,
x-15,
∴x=12,
∴A(12,0),
x=1时,y=![]() ×1-15=-13
×1-15=-13![]() ,共有13个纵坐标、横坐标都是整数的点,
,共有13个纵坐标、横坐标都是整数的点,
同理x=2时,y=-12![]() ,共有12个纵坐标、横坐标都是整数的点,
,共有12个纵坐标、横坐标都是整数的点,
x=3时,y=-11![]() ,共有11个纵坐标、横坐标都是整数的点,
,共有11个纵坐标、横坐标都是整数的点,
x=4时,y=-10,共有10个纵坐标、横坐标都是整数的点,
x=5时,y=-8![]() ,有8个纵坐标、横坐标都是整数的点,
,有8个纵坐标、横坐标都是整数的点,
x=6时,y=-7![]() ,有7个纵坐标、横坐标都是整数的点,
,有7个纵坐标、横坐标都是整数的点,
x=7时,y=-6![]() ,有6个纵坐标、横坐标都是整数的点,
,有6个纵坐标、横坐标都是整数的点,
x=8时,y=-5,共有5个纵坐标、横坐标都是整数的点,
x=9时,y=-3![]() ,共有3个纵坐标、横坐标都是整数的点,
,共有3个纵坐标、横坐标都是整数的点,
x=10时,y=-2![]() ,共有2个纵坐标、横坐标都是整数的点,
,共有2个纵坐标、横坐标都是整数的点,
x=11时,y=-1![]() ,共有1个纵坐标、横坐标都是整数的点,
,共有1个纵坐标、横坐标都是整数的点,
x=12时,y=0,共有1个即A点,纵坐标、横坐标都是整数的点,
在x轴上的点(A除外)有11个,在y轴上的点有1+15=16个.
在△OAB内部(包括边界),纵坐标、横坐标都是整数的点有13+12+11+10+8+7+6+5+3+2+1+1+11+16=106,
故答案为:106.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小玉有5张写着不同数字的卡片,请你按要求抽出卡片,完成下列问题:
-3 -5 0 +3 +4
(1)从中抽出2张卡片,使这2张卡片上的数字的乘积最大,则应如何抽取?最大的乘积是多少?
(2)从中抽出2张卡片,使这2张卡片上的数字相除的商最小,则应如何抽取?最小的商是多少?
(3)从中抽出2张卡片,使这2张卡片上的数字经过加、减、乘、除、乘方中的一种运算后,组成一个最大的数,则应如何抽取?最大的数是多少?
(4)从中抽出4张卡片,用学过的运算方法,要使结果为24,则应如何抽取?写出运算式子(一种即可).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=15,AC=13,BC边上的高AD=12,则BC的长为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=2x+2a与y=-x+b的图象都经过点A(-2,a),且与x轴分别交于B,C两点,则△ABC的面积为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠AOB=108°,OE是∠AOB的平分线,OC在∠AOE内.
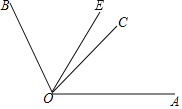
(1)若∠COE=
 ∠AOE,求∠AOC的度数;
∠AOE,求∠AOC的度数;(2)若∠BOC-∠AOC=72°,则OB与OC有怎样的位置关系?为什么?
-
科目: 来源: 题型:
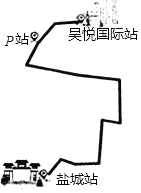
查看答案和解析>>【题目】常州每年举行一次“一袋牛奶的暴走”公益活动,用步行的方式募集善款,其中挑战型路线”的起点是淹城站,并沿着规定的线路到达终点吾悦国际站.甲、乙两组市民从起点同时出发,已知甲组的速度为6km/h,乙组的速度为5km/h,当甲组到达终点后,立即以3km/h的速度按原线路返回,并在途中的P站与乙组相遇,P站与吾悦国际站之间的路程为1.5km
(1)求“挑战型路线”的总长;
(2)当甲组到达终点时,乙组离终点还有多少路程?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把矩形ABCD对折,折痕为MN , 矩形DMNC与矩形ABCD相似,已知AB=4.
(1)求AD的长;
(2)求矩形DMNC与矩形ABCD的相似比.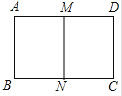
相关试题

