【题目】如图,小玉有5张写着不同数字的卡片,请你按要求抽出卡片,完成下列问题:
-3 -5 0 +3 +4
(1)从中抽出2张卡片,使这2张卡片上的数字的乘积最大,则应如何抽取?最大的乘积是多少?
(2)从中抽出2张卡片,使这2张卡片上的数字相除的商最小,则应如何抽取?最小的商是多少?
(3)从中抽出2张卡片,使这2张卡片上的数字经过加、减、乘、除、乘方中的一种运算后,组成一个最大的数,则应如何抽取?最大的数是多少?
(4)从中抽出4张卡片,用学过的运算方法,要使结果为24,则应如何抽取?写出运算式子(一种即可).
参考答案:
【答案】(1)15;(2)-![]() ;(3)625;(4))(答案不唯一)如抽取-3,-5,0,+3,运算式子为{0-[(-3)+(-5)]}×(+3)=24.
;(3)625;(4))(答案不唯一)如抽取-3,-5,0,+3,运算式子为{0-[(-3)+(-5)]}×(+3)=24.
【解析】
思路点拨:(1)观察这五个数,要找乘积最大的就要找符号相同且数值最大的数,所以选-3和-5;
(2)2张卡片上数字相除的商最小就要找符号不同,且分母越大越好,分子越小越好,所以就要选3和-5,且-5为分母;
(3)这2张卡片上数字组成一个最大的数,除了有个位、十位相乘之外,还有乘方;
(4)利用加减乘除来连接,答案不唯一.
试题
解:(1)抽取![]() ;
;![]()
(2)抽取![]() ;
;![]()
(3)抽取![]() ;
;![]()
(4)答案不唯一;例如抽取-3,-5,3,4;![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2).
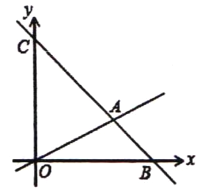
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)在y轴的负半轴上是否存在点M,使△ABM是以AB为直角边的直角角形?如果存在,求出点M的坐标;如果不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(3分)如图,在等边△ABC中,AB=10,BD=4,BE=2,点P从点E出发沿EA方向运动,连接PD,以PD为边,在PD右侧按如图方式作等边△DPF,当点P从点E运动到点A时,点F运动的路径长是( )
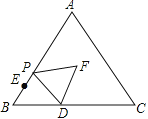
A. 8 B. 10 C. 3π D. 5π
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)如图,已知线段AB上有两点C,D,且AC=BD,M,N分别是线段AC,AD的中点,若AB=acm,AC=BD=bcm,且a,b满足(a-10)2+
 =0.
=0.
(1)求AB,AC的长度;
(2)求线段MN的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=15,AC=13,BC边上的高AD=12,则BC的长为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=2x+2a与y=-x+b的图象都经过点A(-2,a),且与x轴分别交于B,C两点,则△ABC的面积为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=
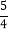 x-15的图象与x轴,y轴分别交于点A,B,O为坐标原点,则在△OAB内部(包括边界),纵坐标、横坐标都是整数的点(整点)共有_________个.
x-15的图象与x轴,y轴分别交于点A,B,O为坐标原点,则在△OAB内部(包括边界),纵坐标、横坐标都是整数的点(整点)共有_________个.
相关试题

