【题目】一元二次方程x2﹣4x+4=0的根的情况为( )
A.只有一个实数根
B.有两个不相等的实数根
C.有两个相等的实数根
D.没有实数根
参考答案:
【答案】C
【解析】解:∵一元二次方程x2﹣4x+4=0,
∴△=(﹣4)2﹣4×1×4=0,
∴方程有两相等实数根.
故选:C.
【考点精析】本题主要考查了求根公式的相关知识点,需要掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知平面直角坐标中有一点M(2﹣a,3a+6),点M到两坐标轴的距离相等,求M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 的对称轴为直线
的对称轴为直线 ,与
,与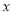 轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:
轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:
①
 ;② 方程
;② 方程 的两个根是
的两个根是 ;③
;③  ;④当
;④当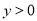 时,
时,  的取值范围是
的取值范围是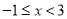 ;⑤ 当
;⑤ 当 时,
时,  随
随 增大而增大;其中结论正确有____.
增大而增大;其中结论正确有____. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.﹣a6(﹣a)3=a8
B.(﹣3m﹣1)(3m﹣1)=﹣9m2+1
C.(x﹣2y)2=x2﹣4y2
D.[(﹣2x)2]3=﹣64x6 -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
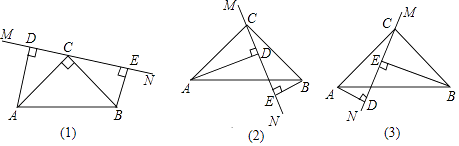
(1)当直线MN绕点C旋转到图(1)的位置时, 求证:①△ADC≌△CEB.②DE=AD+BE;
(2)当直线MN绕点C旋转到图(2)的位置时,求证:DE=AD﹣BE;
(3)当直线MN绕点C旋转到图(3)的位置时,请直接写出DE,AD,BE之间的等量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,∠A=60°,AB=12cm,若点P从点B出发以2cm/s的速度向点A运动,点Q从点A出发以1cm/s的速度向点C运动,设P、Q分别从点B、A同时出发,运动的时间为ts.
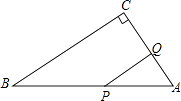
(1)用含t的式子表示线段AP、AQ的长;
(2)当t为何值时,△APQ是以PQ为底边的等腰三角形?
(3)当t为何值时,PQ∥BC? -
科目: 来源: 题型:
查看答案和解析>>【题目】一组数:2,1,3,x,11,y,128,…,其中任意三个连续的数a,b,c满足c=a2﹣b,例如第三个数3=22﹣1,那么这组数中的x、y分别为_____.
相关试题

