【题目】如图,抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,与
,与![]() 轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:
轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:

①![]() ;② 方程
;② 方程![]() 的两个根是
的两个根是![]() ;③
;③ ![]() ;④当
;④当![]() 时,
时, ![]() 的取值范围是
的取值范围是![]() ;⑤ 当
;⑤ 当![]() 时,
时, ![]() 随
随![]() 增大而增大;其中结论正确有____.
增大而增大;其中结论正确有____.
参考答案:
【答案】①②⑤
【解析】试题解析:∵抛物线与x轴有2个交点,
∴b2-4ac>0,所以①正确;
∵抛物线的对称轴为直线x=1,
而点(-1,0)关于直线x=1的对称点的坐标为(3,0),
∴方程ax2+bx+c=0的两个根是x1=-1,x2=3,所以②正确;
∵x=-![]() =1,即b=-2a,
=1,即b=-2a,
而x=-1时,y=0,即a-b+c=0,
∴a+2a+c=0,所以③错误;
∵抛物线与x轴的两点坐标为(-1,0),(3,0),
∴当-1<x<3时,y>0,所以④错误;
∵抛物线的对称轴为直线x=1,
∴当x<1时,y随x增大而增大,所以⑤正确.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对非负实数
 “四舍五入”到个位的值记为
“四舍五入”到个位的值记为  . 即当n为非负整数时,若
. 即当n为非负整数时,若  ,则
,则  =
=  . 如:
. 如:  =3,
=3,  =4,…根据以上材料,解决下列问题:
=4,…根据以上材料,解决下列问题:
(1)填空 = ,
= ,  =;
=;
(2)若 ,则
,则  的取值范围是;
的取值范围是;
(3)求满足 的所有非负实数
的所有非负实数  的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了倡导绿色出行,某市政府2016年投资了320万元,首期建成120个公共自行车站点,配置2500辆公共自行车,2017年又投资了104万元新建了40个公共自行车站点,配置800辆公共自行车. (注:从2016年起至2020年,每个站点的造价和公共自行车的单价每年都保持不变)
(1)请问每个站点的造价和公共自行车的单价分别是多少万元?
(2)若到2020年该市政府将再建造 个新公共自行车站点和配置
个新公共自行车站点和配置  辆公共自行车,并且公共自行车数量不超过新公共自行车站点数量的23倍,并且再建造的新公共自行车站点不超过102个,市政府共有几种选择方案,哪种方案市政府投入的资金最少?
辆公共自行车,并且公共自行车数量不超过新公共自行车站点数量的23倍,并且再建造的新公共自行车站点不超过102个,市政府共有几种选择方案,哪种方案市政府投入的资金最少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知平面直角坐标中有一点M(2﹣a,3a+6),点M到两坐标轴的距离相等,求M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.﹣a6(﹣a)3=a8
B.(﹣3m﹣1)(3m﹣1)=﹣9m2+1
C.(x﹣2y)2=x2﹣4y2
D.[(﹣2x)2]3=﹣64x6 -
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2﹣4x+4=0的根的情况为( )
A.只有一个实数根
B.有两个不相等的实数根
C.有两个相等的实数根
D.没有实数根 -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
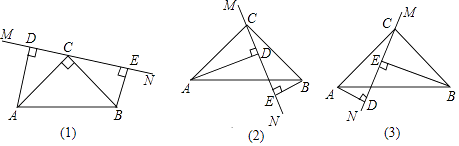
(1)当直线MN绕点C旋转到图(1)的位置时, 求证:①△ADC≌△CEB.②DE=AD+BE;
(2)当直线MN绕点C旋转到图(2)的位置时,求证:DE=AD﹣BE;
(3)当直线MN绕点C旋转到图(3)的位置时,请直接写出DE,AD,BE之间的等量关系.
相关试题

