【题目】某商店试销一种成本为10元的文具.经试销发现,每天销售件数y(件)是每件销售价格x (元)的一次函数,且当每件按15元的价格销售时,每天能卖出50件;当每件按20元的价格销售时,每天能卖出40件.
(1)试求y关于x的函数解析式(不用写出定义域);
(2)如果每天要通过销售该种文具获得450元的利润,那么该种文具每件的销售价格应该定为多少元?(不考虑其他因素)
参考答案:
【答案】(1)y=-2x+80;(2)该种文具每件的销售价格应该定为25元.
【解析】
(1)设出一次函数解析式y=kx+b,用待定系数法建立关于k和b的方程组,解之即可;
(2)按照等量关系“每月获得的利润=(销售价格-进价)×销售件数”列出方程,求解即可.
(1)由题意,知:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
设所求一次函数解析式为![]() .
.
由题意得:![]() 解得:
解得:![]()
∴所求的![]() 关于
关于![]() 的函数解析式为
的函数解析式为![]() .
.
(2)由题意,可得:![]()
解得:![]()
答:该种文具每件的销售价格应该定为25元.
-
科目: 来源: 题型:
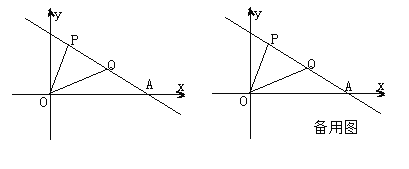
查看答案和解析>>【题目】已知一次函数y=kx+b的图象过P(1,4),Q(4,2)两点,且与x轴交于A点.
(1)求A点坐标;
(2)已知点M在x轴上,若使MP+MQ的值最小,求点M的坐标及MP+MQ的最小值;
(3)在(2)的条件下,在坐标平面内是否还存在一点N,使M,N,A,Q四点恰好构成平行四边形,若存在请求出点N的坐标,若不存在请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
 与射线
与射线 平行,
平行, .点
.点 是直线
是直线 上一动点,过点
上一动点,过点 作
作 交射线
交射线 于点
于点 ,连接
,连接 .作
.作 交直线
交直线 于点
于点 平分
平分 ,点
,点 都在点
都在点 的右侧.
的右侧.
 求
求 的度数;
的度数; 若
若 ,求
,求 的度数;
的度数; 把题中条件“射线
把题中条件“射线 ”改为“直线
”改为“直线 ” ,条件点
” ,条件点 都在点
都在点 的右侧”改为“点
的右侧”改为“点 ,
, ,都在点
,都在点 的左侧”,请你在图2中画出
的左侧”,请你在图2中画出 ,并直接写出
,并直接写出 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某公司计划用32m长的材料沿墙建造的长方形仓库,仓库的一边靠墙,已知墙长16m,设长方形的宽AB为xm.

(1)用x的代数式表示长方形的长BC;
(2)能否建造成面积为120㎡的长方形仓库?若能,求出长方形仓库的长和宽;若不能,请说明理由;
(3)能否建造成面积为160㎡的长方形仓库?若能,求出长方形仓库的长和宽;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,货轮O在航行过程中,发现灯塔A在它北偏东30°的方向上,海岛B在它南偏东60°方向上.则下列结论:
①∠NOA=30°;
②图中∠NOB的补角有两个,分别是∠SOB和∠EOA;
③图中有4对互余的角;
④货轮O在海岛B的西偏北30°的方向上.
其中正确结论的个数有( )

A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】温度通常有两种表示方法:华氏度(单位:
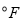 )与摄氏度(单位:
)与摄氏度(单位: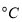 ).已知华氏度数y与摄氏度数x之间是一次函数关系.下表列出了部分华氏度与摄氏度之间的对应关系.
).已知华氏度数y与摄氏度数x之间是一次函数关系.下表列出了部分华氏度与摄氏度之间的对应关系.摄氏度数x(
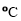 )
)…
0
…
35
…
100
…
华氏度数y(
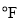 )
)…
32
…
95
…
212
…
(1)选用表格中给出的数据,求y关于x的函数解析式(不需要写出该函数的定义域);
(2)已知某天的最低气温是
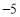
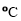 ,求与之对应的华氏度数.
,求与之对应的华氏度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=80°,∠BOC=20°,OE平分∠AOC,则∠AOE=_____.
相关试题

