【题目】2020年1月以来,由于新型冠状病毒(COVID-19)的肆虐,口罩市场出现热卖,某旗舰网店用8000元购进甲、乙两种口罩,销售完后共获利2800元,进价和售价如右表:
品名 | 甲种口罩 | 乙种口罩 |
进价(元/袋) | 20 | 25 |
售价(元/袋) | 26 | 35 |
(1)求该网店购进甲、乙两种口罩各多少袋?
(2)该网店第二次以原价购进甲、乙、两种口罩,购进乙种口罩袋数不变,而购进甲种口罩袋数是第一次的2倍.甲种口罩按原售价出售,而乙种口罩让利销售.若两种口罩销售完毕,要使第二次销售活动获利不少于3680元,乙种口罩最低售价为每袋多少元?
参考答案:
【答案】(1)该网店购进甲种口罩200袋,乙种口罩160袋;(2)乙种口罩最低售价为每袋33元
【解析】
(1)分别根据旗舰网店用8000元购进甲、乙两种口罩,销售完后共获利2800元,得出等式组成方程求出即可;
(2)根据甲种口罩袋数是第一次的2倍,要使第二次销售活动获利不少于3680元,得出不等式求出即可.
设该商店购进甲种口罩x袋,乙种口罩y袋,
根据题意得:![]() ,
,
即
由①,得4x+5y=1600③
由②,得3x+5y=1400④
③-④,得x=200
将x=200代入③,得y=160
答:该网店购进甲种口罩200袋,乙种口罩160袋.
故答案为:该网店购进甲种口罩200袋,乙种口罩160袋.
(2)设乙种口罩每袋售价z元,根据题意得出:
![]()
解得:z≥33
答:乙种口罩每袋售价为每袋33元.
故答案为:乙种口罩最低售价为每袋33元
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于点E,交AC于点F,过点O作OD⊥AC于点D,下列四个结论:①BE=EF-CF;②∠BOC=90°+
 ∠A;③点O到△ABC各边的距离相等;④设OD=m,AE+AF=n,则S△AEF=
∠A;③点O到△ABC各边的距离相等;④设OD=m,AE+AF=n,则S△AEF= mn,其中正确的结论是______.(填所有正确的序号)
mn,其中正确的结论是______.(填所有正确的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】 已知,如图,点C、D在⊙O上,直径AB=6
 ,弦AC、BD相交于点E . 若CE=BC , 则阴影部分面积为( )
,弦AC、BD相交于点E . 若CE=BC , 则阴影部分面积为( ) 
A.
B.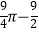
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,有两边长分别为15和13,第三边上的高为12,则第三边长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,AB∥CD,点E,F分别在直线CD,AB上,∠BEC=2∠BEF,过点A作AG⊥BE的延长线交于点G,交CD于点N,AK平分∠BAG,交EF于点H,交BE于点M.
(1)直接写出∠AHE,∠FAH,∠KEH之间的关系:________;
(2)若∠BEF=
 ∠BAK,求∠AHE;
∠BAK,求∠AHE;(3)如图2,在(2)的条件下,将△KHE绕着点E以每秒5°的速度逆时针旋转,旋转时间为t,当KE边与射线ED重合时停止,则在旋转过程中,当△KHE的其中一边与△ENG的某一边平行时,直接写出此时t的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,对于点P(x,y),我们把点
 (-y+1,x+1)叫做点P伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An,….若点A1的坐标为(2,4),点A2017的坐标为 ( )
(-y+1,x+1)叫做点P伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An,….若点A1的坐标为(2,4),点A2017的坐标为 ( )A. (-3,3) B. (-2,-2) C. (3,-1) D. (2,4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC=25,AB=30,D是AB上的一点(不与A、B重合),DE⊥BC,垂足是点E,设BD=x,四边形ACED的周长为y,则下列图象能大致反映y与x之间的函数关系的是( )

A.
B.
C.
D.
相关试题

