【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于点E,交AC于点F,过点O作OD⊥AC于点D,下列四个结论:①BE=EF-CF;②∠BOC=90°+![]() ∠A;③点O到△ABC各边的距离相等;④设OD=m,AE+AF=n,则S△AEF=
∠A;③点O到△ABC各边的距离相等;④设OD=m,AE+AF=n,则S△AEF=![]() mn,其中正确的结论是______.(填所有正确的序号)
mn,其中正确的结论是______.(填所有正确的序号)

参考答案:
【答案】①②③④
【解析】
由在△ABC中,∠ABC和∠ACB的平分线相交于点O,根据角平分线的定义与三角形内角和定理,即可求得②∠BOC=90°+![]() ∠A正确;由平行线的性质和角平分线的定义得出△BEO和△CFO是等腰三角形得出BE=EF-CF故①正确;由角平分线的性质得出点O到△ABC各边的距离相等,故③正确;由角平分线定理与三角形面积的求解方法,即可求得③设OD=m,AE+AF=n,则S△AEF=
∠A正确;由平行线的性质和角平分线的定义得出△BEO和△CFO是等腰三角形得出BE=EF-CF故①正确;由角平分线的性质得出点O到△ABC各边的距离相等,故③正确;由角平分线定理与三角形面积的求解方法,即可求得③设OD=m,AE+AF=n,则S△AEF=![]() mn,故④正确.
mn,故④正确.
解:∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,∠A+∠ABC+∠ACB=180°,
∠ACB,∠A+∠ABC+∠ACB=180°,
∴∠OBC+∠OCB=90°-![]() ∠A,
∠A,
∴∠BOC=180°-(∠OBC+∠OCB)=90°+![]() ∠A;故②正确;
∠A;故②正确;
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=∠OBE,∠OCB=∠OCF,
∵EF∥BC,
∴∠OBC=∠EOB,∠OCB=∠FOC,
∴∠EOB=∠OBE,∠FOC=∠OCF,
∴BE=OE,CF=OF,
∴EF=OE+OF=BE+CF,
即BE=EF-CF.故①正确;
过点O作OM⊥AB于M,作ON⊥BC于N,连接OA,
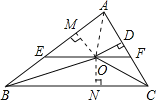
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴ON=OD=OM=m,
∴S△AEF=S△AOE+S△AOF=![]() AEOM+
AEOM+![]() AFOD=
AFOD=![]() OD(AE+AF)=
OD(AE+AF)=![]() mn;故④正确;
mn;故④正确;
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴点O到△ABC各边的距离相等,故③正确.
故答案为①②③④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A变换为点D,点E、F分别是B、C的对应点.
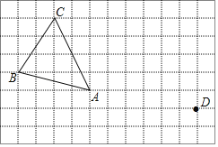
(1)△ABC的面积为______;
(2)请画出平移后的△DEF;
(3)利用格点画出△DEF的高FG(点G为垂足);
(4)若连接AD、CF,则这两条线段之间的关系是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程组:
(1)
 ; (2)
; (2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,l1反映了某公司销售一种医疗器械的销售收入(万元)与销售量(台)之间的关系,l2反映了该公司销售该种医疗器械的销售成本(万元)与销售量(台)之间的关系.当销售收入大于销售成本时,该医疗器械才开始赢利.根据图象,则下列判断中错误的是( )

A. 当销售量为4台时,该公司赢利4万元
B. 当销售量多于4台时,该公司才开始赢利
C. 当销售量为2台时,该公司亏本1万元
D. 当销售量为6台时,该公司赢利1万元
-
科目: 来源: 题型:
查看答案和解析>>【题目】 已知,如图,点C、D在⊙O上,直径AB=6
 ,弦AC、BD相交于点E . 若CE=BC , 则阴影部分面积为( )
,弦AC、BD相交于点E . 若CE=BC , 则阴影部分面积为( ) 
A.
B.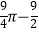
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,有两边长分别为15和13,第三边上的高为12,则第三边长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2020年1月以来,由于新型冠状病毒(COVID-19)的肆虐,口罩市场出现热卖,某旗舰网店用8000元购进甲、乙两种口罩,销售完后共获利2800元,进价和售价如右表:
品名
价格甲种口罩
乙种口罩
进价(元/袋)
20
25
售价(元/袋)
26
35
(1)求该网店购进甲、乙两种口罩各多少袋?
(2)该网店第二次以原价购进甲、乙、两种口罩,购进乙种口罩袋数不变,而购进甲种口罩袋数是第一次的2倍.甲种口罩按原售价出售,而乙种口罩让利销售.若两种口罩销售完毕,要使第二次销售活动获利不少于3680元,乙种口罩最低售价为每袋多少元?
相关试题

