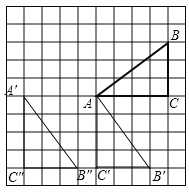
【题目】 如图，正方形网格中的每个小正方形的边长都是1，每个小正方形的顶点叫作格点．△ABC的三个顶点A，B，C都在格点上，将△ABC绕点A按顺时针方向旋转90°得到△AB′C′．

（1）在正方形网格中，画出△AB'C′；

（2）画出△AB′C′向左平移4格后的△A′B″C″；

（3）计算线段AB在变换到AB′的过程中扫过区域的面积．

参考答案：

【答案】（1）见解析；（2）见解析；（3）．

【解析】

（1）直接利用旋转的性质得出对应点位置进而得出答案；

（2）利用平移的性质得出对应点位置进而得出答案；

（3）利用扇形面积求法得出答案．

（1）如图所示：△AB'C'即为所求；

（2）如图所示：△A'B″C″即为所求；

（3）由勾股定理得AB=5，线段AB在变换到AB'的过程中扫过区域的面积为：π．

关闭