【题目】如图,AD是△ABC的中线,tanB= ![]() ,cosC=
,cosC= ![]() ,AC=
,AC= ![]() .求:
.求: 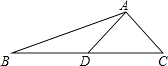
(1)BC的长;
(2)sin∠ADC的值.
参考答案:
【答案】
(1)解:过点A作AE⊥BC于点E,
∵cosC= ![]() ,
,
∴∠C=45°,
在Rt△ACE中,CE=ACcosC=1,
∴AE=CE=1,
在Rt△ABE中,tanB= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴BE=3AE=3,
∴BC=BE+CE=4

(2)解:∵AD是△ABC的中线,
∴CD= ![]() BC=2,
BC=2,
∴DE=CD﹣CE=1,
∵AE⊥BC,DE=AE,
∴∠ADC=45°,
∴sin∠ADC= ![]() .
.
【解析】(1)过点A作AE⊥BC于点E,根据cosC= ![]() ,求出∠C=45°,求出AE=CE=1,根据tanB=
,求出∠C=45°,求出AE=CE=1,根据tanB= ![]() ,求出BE的长即可;(2)根据AD是△ABC的中线,求出BD的长,得到DE的长,得到答案.
,求出BE的长即可;(2)根据AD是△ABC的中线,求出BD的长,得到DE的长,得到答案.
【考点精析】解答此题的关键在于理解解直角三角形的相关知识,掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).
-
科目: 来源: 题型:
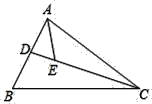
查看答案和解析>>【题目】在△ABC中,∠ADC=88°,∠B=68°,∠ACD=∠BCD,AE平分∠BAC,则∠AED的度数为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在第1个△ABA1中,∠B=40°,∠BAA1=∠BA1A,在A1B上取一点C,延长AA1到A2,使得在第2个△A1CA2中,∠A1CA2=∠A1 A2C;在A2C上取一点D,延长A1A2到A3,使得在第3个△A2DA3中,∠A2DA3=∠A2 A3D;…,按此做法进行下去,第3个三角形中以A3为顶点的内角的度数为 ;第n个三角形中以An为顶点的内角的度数为 .

-
科目: 来源: 题型:
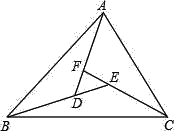
查看答案和解析>>【题目】如图,∠BAD=∠CBE=∠ACF,∠FDE=64°,∠DEF=43°,求△ABC各内角的度数.
-
科目: 来源: 题型:
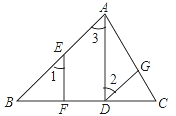
查看答案和解析>>【题目】如图,已知△ABC中,AD⊥BC于点D,E为AB边上任意一点,EF⊥BC于点F,∠1=∠2.求证:DG∥AB.请把证明的过程填写完整.
证明:∵AD⊥BC,EF⊥BC( ),
∴∠EFB=∠ADB=90°(垂直的定义)
∴EF∥ ( )
∴∠1= ( )
又∵∠1=∠2(已知)
∴ ( )
∴DG∥AB( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E为BC边的中点,连接DE.
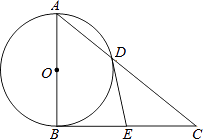
(1)求证:DE与⊙O相切.
(2)若tanC=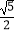 ,DE=2,求AD的长.
,DE=2,求AD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线经过A(﹣1,0),B(5,0),C(0,-
 )三点.
)三点.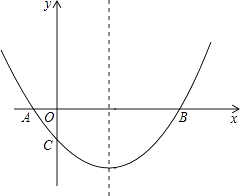
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
相关试题

