【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E为BC边的中点,连接DE. 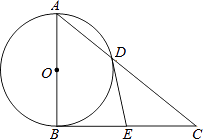
(1)求证:DE与⊙O相切.
(2)若tanC= ![]() ,DE=2,求AD的长.
,DE=2,求AD的长.
参考答案:
【答案】
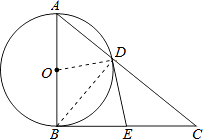
(1)证明:连接DO,DB,
∴OD=OB,
∴∠ODB=∠OBD.
∵AB是直径,
∴∠ADB=90°,
∴∠CDB=90°.
∵E为BC的中点,
∴DE=BE,
∴∠EDB=∠EBD,
∴∠ODB+∠EDB=∠OBD+∠EBD,
即∠EDO=∠EBO.
∵∠ABC=90°,
∴∠EDO=90°.
∴OD⊥ED于点D.
又∵OD是半径,
∴DE为⊙O的切线
(2)解:∵∠BDC=90°,点E为BC的中点,
∴DE= ![]() BC.
BC.
∵DE=2,
∴BC=4.
在直角△ABC中,tanC= ![]() ,
,
∴AB=BC× ![]() =2
=2 ![]() .
.
在直角△ABC中,由勾股定理得到AC=6.
又∵△ABD∽△ACB,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴AD= ![]() .
.
【解析】(1)如图,连接DO、DB.欲证明DE与⊙O相切,只需证得OD⊥DE即可;(2)由“直角三角形斜边上的中线等于斜边的一半”易求DE= ![]() BC=2,则BC=4;然后通过解直角△ABC求得AB=2
BC=2,则BC=4;然后通过解直角△ABC求得AB=2 ![]() 、由勾股定理求得AC=6;最后通过△ABD∽△ACB的对应边成比例求得AD=
、由勾股定理求得AC=6;最后通过△ABD∽△ACB的对应边成比例求得AD= ![]() .
.
【考点精析】关于本题考查的切线的判定定理和相似三角形的判定与性质,需要了解切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAD=∠CBE=∠ACF,∠FDE=64°,∠DEF=43°,求△ABC各内角的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是△ABC的中线,tanB=
 ,cosC=
,cosC= 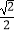 ,AC=
,AC=  .求:
.求: 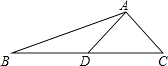
(1)BC的长;
(2)sin∠ADC的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AD⊥BC于点D,E为AB边上任意一点,EF⊥BC于点F,∠1=∠2.求证:DG∥AB.请把证明的过程填写完整.
证明:∵AD⊥BC,EF⊥BC( ),
∴∠EFB=∠ADB=90°(垂直的定义)
∴EF∥ ( )
∴∠1= ( )
又∵∠1=∠2(已知)
∴ ( )
∴DG∥AB( )
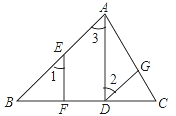
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线经过A(﹣1,0),B(5,0),C(0,-
 )三点.
)三点.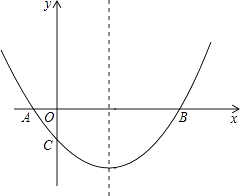
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一个钝角三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“智慧三角形”.如,三个内角分别为120°,40°,20°的三角形是“智慧三角形”.如图,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交射线OB于点C.
(1)∠ABO的度数为_____°,△AOB_____(填“是”或“不是”) “智慧三角形”;
(2)若∠OAC=20°,求证:△AOC为“智慧三角形”;
(3)当△ABC为“智慧三角形”时,求∠OAC的度数.
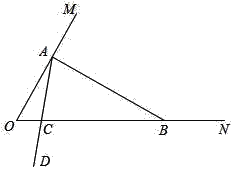
-
科目: 来源: 题型:
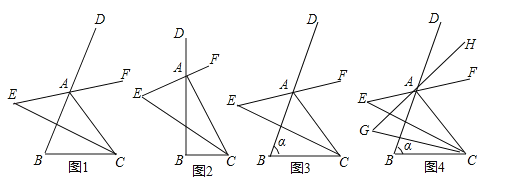
查看答案和解析>>【题目】如图,在△ABC中,分别作其内角∠ACB与外角∠DAC的角平分线,且两条角平分线所在的直线交于点E
(1)填空:①如图1,若∠B=60°,则∠E= ;
②如图2,若∠B=90°,则∠E= ;
(2)如图3,若∠B=α,求∠E的度数;
(3)如图4,仿照(2)中的方法,在(2)的条件下分别作∠EAB与∠ECB的角平分线,且两条角平分线交于点G,求∠G的度数.
相关试题

