【题目】如图,△ABC为等边三角形,D为边BA延长线上一点,连接CD,以CD为一边作等边三角形CDE,连接AE.
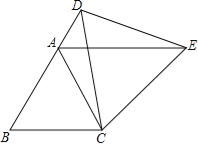
(1)求证:△CBD≌△CAE.
(2)判断AE与BC的位置关系,并说明理由.
参考答案:
【答案】(1)证明见试题解析;(2)AE∥BC,理由见试题解析.
【解析】试题(1)根据等边三角形各内角为60°和各边长相等的性质可证∠ECA=∠DCB,AC=BC,EC=DC,即可证明△ECA≌△DCB;
(2)根据△ECA≌△DCB可得∠EAC=60°,根据内错角相等,平行线平行即可解题.
证明:(1)∵△ABC、△DCE为等边三角形,
∴AC=BC,EC=DC,∠ACB=∠ECD=∠DBC=60°,
∵∠ACD+∠ACB=∠DCB,∠ECD+∠ACD=∠ECA,
∴∠ECA=∠DCB,
在△ECA和△DCB中,
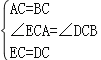 ,
,
∴△ECA≌△DCB(SAS);
(2)∵△ECA≌△DCB,
∴∠EAC=∠DBC=60°,
又∵∠ACB=∠DBC=60°,
∴∠EAC=∠ACB=60°,
∴AE∥BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一块直角三角形绿地,两直角边长分别为3m,4m,现在要将绿地扩充成等腰三角形,且扩充时只能延长长为3m的直角边,则扩充后等腰三角形绿地的面积为____m2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某体育用品商场预测某品牌运动服能够畅销,就用32000元购进了一批这种运动服,上市后很快脱销,商场又用68000元购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该商场两次共购进这种运动服多少套?
(2)如果这两批运动服每套的售价相同,且全部售完后总利润不低于20%,那么每套售价至少是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、 B的坐标分别为(0,2),(1,0),直线y=
 x3与y轴交于点C, 与x轴交于点D,
x3与y轴交于点C, 与x轴交于点D,
(1)求直线AB与CD交点E的坐标;
(2)求四边形OBEC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一家蔬菜公司收购到某种绿色蔬菜200吨,准备加工后进行销售,销售后获利的情况如下表所示:
销售方式
粗加工后销售
精加工后销售
每吨获利(元)
500
800
已知该公司的加工能力是:每天能精加工5吨或粗加工15吨,但两种加工不能同时进行.受季节等条件的限制,公司必须在一定时间内将这批蔬菜全部加工后销售完.
(1)如果要求20天刚好加工完200吨蔬菜,则公司应安排几天精加工,几天粗加工?
(2)如果先进行精加工,然后进行粗加工.
①试求出销售利润W元与精加工的蔬菜吨数m之间的函数关系式;
②若要求在不超过16天的时间内,将200吨蔬菜全部加工完后进行销售,则加工这批蔬菜最多获得多少利润?此时如何分配加工时间?
-
科目: 来源: 题型:
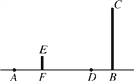
查看答案和解析>>【题目】如图,在一座大厦(图中BC所示)前面30m的地面上,有一盏地灯A照射大厦,身高为1.6m的小亮(图中EF所示)站在大厦和灯之间,若小亮从现在所处位置径直走向大厦,当他走到距离大厦只有5m的D处时停下.
(1)请在图中画出此时小亮的位置(可用线段表示)及他在地灯照射下投在大厦BC上的影子;
(2)请你求出此时小亮的影长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车分别从相距480km的A.B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,结合图象信息解答下列问题:
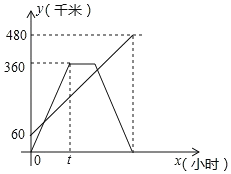
(1)乙车的速度是___千米/时,t=___小时;
(2)求甲车距它出发地的路程y与它出发的时间x的函数关系式,并写出自变量的取值范围;
(3)直接写出两车相距150千米时x的取值.
相关试题

