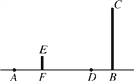
【题目】如图,在一座大厦(图中BC所示)前面30m的地面上,有一盏地灯A照射大厦,身高为1.6m的小亮(图中EF所示)站在大厦和灯之间,若小亮从现在所处位置径直走向大厦,当他走到距离大厦只有5m的D处时停下.
(1)请在图中画出此时小亮的位置(可用线段表示)及他在地灯照射下投在大厦BC上的影子;
(2)请你求出此时小亮的影长.
参考答案:
【答案】(1)作图见解析;(2)小亮此时的影长是1.92m.
【解析】试题分析:(1)根据中心投影的特点可知,连接物体和它影子的顶端所形成的直线必定经过点光源,即由点光源出发连接小亮顶部的直线与大厦相交即可找到小亮影子的顶端,(2)由平行可得: △ADN∽△ABM,再根据相似三角形的性质对应边成比例求解即可.
试题解析:(1)如图所示:BM即为所求,
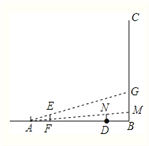
(2)∵DN∥BC,
∴△ADN∽△ABM,
∴![]() ,
,
∵AB=30m,BD=5m,DN=1.6m,则AD=25m,
∴![]() ,
,
解得:BM=1.92,
答:此时小亮在地灯A照射下投在大厦BC上的影长为1.92m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、 B的坐标分别为(0,2),(1,0),直线y=
 x3与y轴交于点C, 与x轴交于点D,
x3与y轴交于点C, 与x轴交于点D,
(1)求直线AB与CD交点E的坐标;
(2)求四边形OBEC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为等边三角形,D为边BA延长线上一点,连接CD,以CD为一边作等边三角形CDE,连接AE.
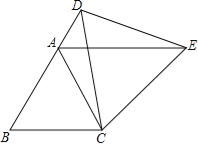
(1)求证:△CBD≌△CAE.
(2)判断AE与BC的位置关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一家蔬菜公司收购到某种绿色蔬菜200吨,准备加工后进行销售,销售后获利的情况如下表所示:
销售方式
粗加工后销售
精加工后销售
每吨获利(元)
500
800
已知该公司的加工能力是:每天能精加工5吨或粗加工15吨,但两种加工不能同时进行.受季节等条件的限制,公司必须在一定时间内将这批蔬菜全部加工后销售完.
(1)如果要求20天刚好加工完200吨蔬菜,则公司应安排几天精加工,几天粗加工?
(2)如果先进行精加工,然后进行粗加工.
①试求出销售利润W元与精加工的蔬菜吨数m之间的函数关系式;
②若要求在不超过16天的时间内,将200吨蔬菜全部加工完后进行销售,则加工这批蔬菜最多获得多少利润?此时如何分配加工时间?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车分别从相距480km的A.B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,结合图象信息解答下列问题:
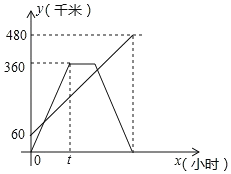
(1)乙车的速度是___千米/时,t=___小时;
(2)求甲车距它出发地的路程y与它出发的时间x的函数关系式,并写出自变量的取值范围;
(3)直接写出两车相距150千米时x的取值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的一点,F为AB边上一点,连接CF,交BE于点D,且∠ACF=∠CBE,CG平分∠ACB交BD于点G,
(1)如图1,求证:CF=BG;
(2)如图2,延长CG交AB于H,连接AG,过点C作CP∥AG交BE的延长线于点P,
求证:PB=CP+CF;
(3)如图3,在(2)间的条件下,当∠GAC=2∠FCH时,若S△AEG=3
 ,BG=6,求AC的长.
,BG=6,求AC的长.
-
科目: 来源: 题型:
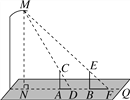
查看答案和解析>>【题目】晚饭后,小聪和小军在社区广场散步,小聪问小军:“你有多高?”小军一时语塞.小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高.于是,两人在灯下沿直线NQ移动,如图,当小聪正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小军正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小聪的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小军身高BE的长(结果精确到0.01米).
相关试题

